Question

Evaluate $\dfrac{1}{{\sqrt 3 }}\sec {60^ \circ } - {\text{cosec}}{60^ \circ }$.

Answer 1

We know the magnitude of the trigonometric ratios of standard angles. Therefore, substitute the values of $\sec {60^ \circ }$ and ${\text{cosec}}{60^ \circ }$ in the given expression to find the required answer.

Formula used: Trigonometric ratios of the standard angles are given by:

| 0°| 30°| 45°| 60°| 90°
---|---|---|---|---|---
sinx| 0| $\dfrac{1}{2}$ | $\dfrac{1}{{\sqrt 2 }}$ | $\dfrac{{\sqrt 3 }}{2}$ | 1
cosx| 1| $\dfrac{{\sqrt 3 }}{2}$| $\dfrac{1}{{\sqrt 2 }}$| $\dfrac{1}{2}$| 0
tanx| 0| $\dfrac{1}{{\sqrt 3 }}$ | 1| $\sqrt 3$| Undefined
cotx| undefined| $\sqrt 3$| 1| $\dfrac{1}{{\sqrt 3 }}$| 0
cosecx| undefined| 2| $\sqrt 2$| $\dfrac{2}{{\sqrt 3 }}$| 1
secx| 1| $\dfrac{2}{{\sqrt 3 }}$| $\sqrt 2$| 2| Undefined

Therefore, $\sec {60^ \circ } = 2$ and ${\text{cosec}}{60^ \circ } = \dfrac{2}{{\sqrt 3 }}$

Complete step-by-step solution:
From the above table, let’s recall that $\sec {60^ \circ } = 2$ and ${\text{cosec}}{60^ \circ } = \dfrac{2}{{\sqrt 3 }}$
Therefore, substituting the values in the given expression, we get
$\dfrac{1}{{\sqrt 3 }}\sec {60^ \circ } - {\text{cosec}}{60^ \circ }$
$= \dfrac{1}{{\sqrt 3 }} \times 2 - \dfrac{2}{{\sqrt 3 }}$
$= \dfrac{2}{{\sqrt 3 }} - \dfrac{2}{{\sqrt 3 }}$
$= 0$

Therefore the value of $\dfrac{1}{{\sqrt 3 }}\sec {60^ \circ } - {\text{cosec}}{60^ \circ }$ is 0.

Note: Note the following important formulae of trigonometry:
$\cos x = \dfrac{1}{{\sec x}}$ , $\sin x = \dfrac{1}{{\cos ecx}}$ , $\tan x = \dfrac{1}{{\cot x}}$
${\sin ^2}x + {\cos ^2}x = 1$
${\sec ^2}x - {\tan ^2}x = 1$
${\operatorname{cosec} ^2}x - {\cot ^2}x = 1$
$\sin ( - x) = - \sin x$
$\cos ( - x) = \cos x$
$\tan ( - x) = - \tan x$
$\sin \left( {2n\pi \pm x} \right) = \sin x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
$\cos \left( {2n\pi \pm x} \right) = \cos x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
$\tan \left( {n\pi \pm x} \right) = \tan x{\text{ , period }}\pi {\text{ or 18}}{0^ \circ }$
Sign convention:

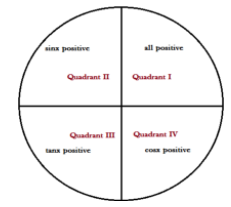
$\sin 2x = 2\sin x\cos x$
$\cos 2x = {\cos ^2}x - {\sin ^2}x = 1 - 2{\sin ^2}x = 2{\cos ^2}x - 1$
$\tan 2x = \dfrac{{2\tan x}}{{1 - {{\tan }^2}x}} = \dfrac{2}{{\cot x - \tan x}}$