Question

Evaluate $\cos \left( {{{\tan }^{ - 1}}x} \right) =$
1). $\sqrt {1 + {x^2}}$
2). $\dfrac{1}{{\sqrt {1 + {x^2}} }}$
3). $1 + {x^2}$
4). None of these

Answer 1

In order to solve the given equation, consider ${\tan ^{ - 1}}x$ to be any variable, then using the properties of triangles like Pythagoras theorem and trigonometric ratios like $\tan \theta = \dfrac{{perpendicular}}{{base}}$, find the value of the variable, solve further and get the results.
Formula used:
$\tan \theta = \dfrac{{perpendicular}}{{base}}$
$\cos \theta = \dfrac{{base}}{{hypotenuse}}$

Complete step-by-step solution:
We are given the value $\cos \left( {{{\tan }^{ - 1}}x} \right)$.
Considering the value of ${\tan ^{ - 1}}x$ to be $\theta$ , which can be numerically written as:
${\tan ^{ - 1}}x = \theta$
Multiplying both the sides by $\tan$, we get:
$\tan \left( {{{\tan }^{ - 1}}x} \right) = \tan \theta$ ……………………..(1)
Since, we know that in $\tan \left( {{{\tan }^{ - 1}}x} \right) = \tan \theta$, the $\tan$ will cancel ${\tan ^{ - 1}}x$, so we are left with $\tan \left( {{{\tan }^{ - 1}}x} \right) = x$, So substituting this value in equation (1), we get:
$\tan \left( {{{\tan }^{ - 1}}x} \right) = \tan \theta$
$\Rightarrow x = \tan \theta$
Which can also be written as:
$\Rightarrow \tan \theta = x$ …………………………..(2)
From Trigonometric ratios, we know that:
$\Rightarrow \tan \theta = \dfrac{{perpendicular}}{{base}}$ ……..(3)
Equating equation (2) and equation (3), we get:
$\Rightarrow x = \dfrac{{perpendicular}}{{base}}$
$x$ can also be written as $\dfrac{x}{1}$, as anything divided by $1$ , gives the same answer:
Therefore,
$\Rightarrow \dfrac{x}{1} = \dfrac{{perpendicular}}{{base}}$
Drawing a right-angled triangle ABC with perpendicular of $x$ and base to be $1$, perpendicular to each other at B:

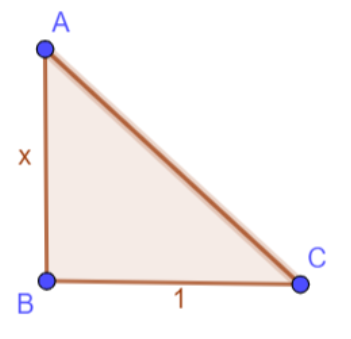
Since, it is a right - angled triangle, so we can apply Pythagoras theorem:
$A{B^2} + B{C^2} = A{C^2}$
Substituting the values, we get:
$\Rightarrow {x^2} + {1^2} = A{C^2}$
Taking square root both the sides, we get:
$\Rightarrow \sqrt {{x^2} + {1^2}} = \sqrt {A{C^2}}$
$\Rightarrow \sqrt {{x^2} + 1} = AC$
$\Rightarrow AC = \sqrt {{x^2} + 1}$
Therefore, hypotenuse $= \sqrt {{x^2} + 1}$.
Since, we were given $\cos \left( {{{\tan }^{ - 1}}x} \right)$, and we considered ${\tan ^{ - 1}}x = \theta$, so substituting ${\tan ^{ - 1}}x = \theta$ in $\cos \left( {{{\tan }^{ - 1}}x} \right)$, we get:
$\Rightarrow \cos \left( {{{\tan }^{ - 1}}x} \right) = \cos \left( \theta \right)$
$\Rightarrow \cos \left( {{{\tan }^{ - 1}}x} \right) = \cos \theta$ …….(4)
From Trigonometric ratios, we know that $\cos \theta = \dfrac{{base}}{{hypotenuse}}$.
And, we can see from the triangle ABC, base $= 1$ and hypotenuse $= \sqrt {{x^2} + 1}$.
Substituting them in $\cos \theta = \dfrac{{base}}{{hypotenuse}}$ , we get:
$\cos \theta = \dfrac{{base}}{{hypotenuse}} = \dfrac{1}{{\sqrt {{x^2} + 1} }}$
$\Rightarrow \cos \theta = \dfrac{1}{{\sqrt {{x^2} + 1} }}$
Substituting this value in equation (4), we get:
$\Rightarrow \cos \left( {{{\tan }^{ - 1}}x} \right) = \cos \theta = \dfrac{1}{{\sqrt {{x^2} + 1} }}$
$\Rightarrow \cos \left( {{{\tan }^{ - 1}}x} \right) = \dfrac{1}{{\sqrt {{x^2} + 1} }}$
Therefore, $\cos \left( {{{\tan }^{ - 1}}x} \right) = \dfrac{1}{{\sqrt {{x^2} + 1} }}$.
Hence, Option 2 is correct.

Note: It’s important to follow the correct steps and solve step by step instead of solving it at once, otherwise it may lead to error. Do not forget to draw the rough diagram of the triangle in order to get the value of the hypotenuse.