Question
Question: Evaluate \[\cos \left( {{{\sin }^{ - 1}}\left( {\dfrac{3}{7}} \right)} \right)\]....
Evaluate cos(sin−1(73)).
Solution
In the given problem, we are required to calculate the cosine of an angle whose sine is given to us. Such problems require basic knowledge of trigonometric ratios and formulae. Besides this, knowledge of concepts of inverse trigonometry is extremely essential to answer these questions correctly.
Formula used:
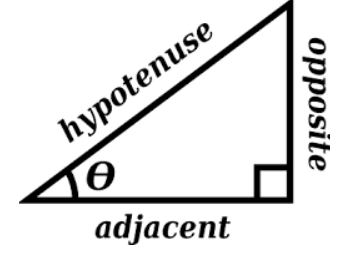
sinθ=HypotenuseOpposite side
cosθ=HypotenuseAdjacent side
Complete step by step solution:
In the given problem, we have to find the value ofcos(sin−1(73)).
Hence, we have to find the cosine of the angle whose sine is given to us as (73).
Let us assume θ to be the concerned angle.
Then, θ=sin−1(73)
Taking sine on both sides of the equation, we get
=sinθ=73
To evaluate the value of the required expression, we must keep in mind the formulae of basic trigonometric ratios.
We know that, sinθ=HypotenusePerpendicularand cosθ=HypotenuseBase.
So, sinθ=HypotenusePerpendicular=73
Let the length of the perpendicular be3x.
Then, length of hypotenuse =7x.
Now, applying Pythagoras Theorem,
(Hypotenuse)2=(Base)2+(Perpendicular)2
=(7x)2=(Base)2+(3x)2
Computing the squares, we get,
=49x2=(Base)2+9x2
=(Base)2=49x2−9x2
=(Base)=40x2
Simplifying the expression by taking the factor appearing twice in the factorisation of the number outside the square root. So, we get,
=(Base)=210x
So, we get Base=210x
Hence, cosθ=7x210x=7210
Therefore, the value ofcos(sin−1(73)) is 7210.
Note:
The given problem can also be solved by use of some basic trigonometric identities such as sin2(θ)+cos2(θ)=1. This method also provides exposure to the applications of trigonometric identities in various mathematical questions.
