Question

Establish the refraction formula for a thin lens:
$\dfrac{1}{f}=\left( \mu -1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$

Answer 1

Consider the lens as two surfaces and not one. The rays are going from denser to rarer medium or vice versa that means a change of medium is there. Also,it is a thin lens so use the formula for thin lens that is thickness approximately null.

Complete step by step answer:

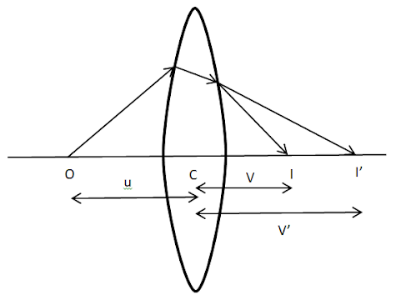
Let’s take a convex lens L having refractive index $\mu$.O is the object placed on the principal axis at a distance of ‘u’ . I’ is the image at a distance of v from the optical centre formed due to refraction at the first surface AB with the radius of curvature ${{R}_{1}}$ and $I$ is the final image at a distance of v’ from the optical centre formed after refraction at the second surface A’B’ with radius of curvature ${{R}_{2}}$.

According to the refraction formula for a convex spherical surface:
$\dfrac{\mu -1}{R}=\dfrac{\mu }{V}-\dfrac{1}{U}$
Where $R$ is the radius of curvature, $\mu$ is the refractive index, $U$ is the object distance and $V$ is the image distance.
For surface AB,we have
$R={{R}_{1}}$,
$V=v’$ as I’ is the image formed after refraction from surface AB.
$\Rightarrow U=u$ (distance of object O )
Substituting these values in the refraction formula, we get
$\dfrac{\mu -1}{{{R}_{1}}}=\dfrac{\mu }{v'}-\dfrac{1}{u}$ --equation 1……(Here $\mu$ is the refractive index of glass with respect to air)

For surface A’B’,we have
$R={{R}_{2}}$,
$\Rightarrow V=v$ as $I$ is the final image formed after refraction from surface A’B’.
$\Rightarrow U=v’$ (Image at $I’$ acts as a virtual object for refraction at A’B’)
Substituting these values in the refraction formula, we get
$\dfrac{\dfrac{1}{\mu }-1}{{{R}_{2}}}=\dfrac{\dfrac{1}{\mu }}{v'}-\dfrac{1}{u}$ (Here $\Rightarrow \dfrac{1}{\mu }$is the refractive index of air with respect to glass)
$\Rightarrow \dfrac{1-\mu }{\mu {{R}_{2}}}=\dfrac{1}{\mu v}-\dfrac{1}{v'}$

Multiplying by $\mu$,we get
\mu \left( \dfrac{1-\mu }{\mu {{R}_{2}}} \right)=\dfrac{\mu }{\mu v}-\dfrac{\mu }{v'} \\\
$\Rightarrow \dfrac{1-\mu }{{{R}_{2}}}=\dfrac{1}{v}-\dfrac{\mu }{v'}$--equation 2
Adding equation 1 and 2, we get
$\left( \mu -1 \right)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]=\dfrac{1}{v}-\dfrac{1}{u}$--equation 3
Now if the focal length of lens L is f, we know that the formula for focal length is
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$--equation 4
Substituting equation 4 in equation 3,we get
$\left( \mu -1 \right)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]=\dfrac{1}{f}$
Hence we establish the formula for refraction of a thin lens:
$\dfrac{1}{f}=\left( \mu -1 \right)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]$

Note: The refractive index of both the surfaces will be different as during the first surface , rays go from rarer to denser medium and in the second surface, rays travel from denser to rarer medium. This is the most common mistake. Treat the lens as two spherical surfaces and apply the refraction formula for spherical convex surface.