Question

Establish a relationship to determine the equivalent resistance R of a combination of three resistors having resistances ${{\text{R}}_{\text{1}}}$, ${{\text{R}}_{\text{2}}}$, and ${{\text{R}}_{3}}$ connected in series. Calculate the equivalent resistance of the combination of three resistors of $2\Omega$, $3\Omega$ and $6\Omega$ joined in parallel.

Answer 1

Hint: In the series connection, the total resistance is equal to the sum of the resistance of each resistor. So, the equivalent resistance will be more than the resistance of each resistor. We can find it from Ohm’s law. In the series connection, the current will be the same throughout the circuit.
In a parallel connection, the total resistance will be less than the resistance of each resistor. We can calculate the equivalent resistance of the parallel connection by using the following formula.
$\dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}$
Formula used:
$\text{V=IR}$, where V is the voltage, I is the current and R is the resistance
$\dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}$, where R is the equivalent resistance and all other terms are resistances of each resistor.

Complete step-by-step answer:

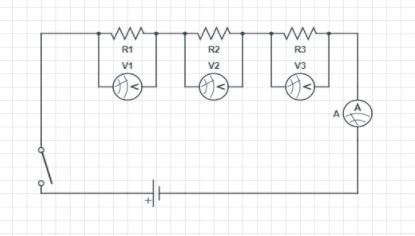
In this diagram we can see, three resistors have been connected in series. To check the potential drop we have connected voltmeters through each resistor.
So, the total potential can be written as,
$\text{V=}{{\text{V}}_{\text{1}}}\text{+}{{\text{V}}_{\text{2}}}\text{+}{{\text{V}}_{\text{3}}}$
To find the resistance, we can use ohm’s law.
${{\text{V}}_{\text{1}}}\text{=I}{{\text{R}}_{\text{1}}}$
${{\text{V}}_{2}}\text{=I}{{\text{R}}_{2}}$
${{\text{V}}_{3}}\text{=I}{{\text{R}}_{3}}$
We can add these potential drops to find out the total voltage.
$\text{V=I}{{\text{R}}_{\text{1}}}\text{+I}{{\text{R}}_{\text{2}}}\text{+I}{{\text{R}}_{\text{3}}}$
$\text{V=I(}{{\text{R}}_{\text{1}}}\text{+}{{\text{R}}_{\text{2}}}\text{+}{{\text{R}}_{\text{3}}})$
From this expression, we can say that current will be the same in a series circuit.
$\text{V=IR}$
i.e. $\text{R}$ is the equivalent resistance of three resistors.
$\text{R=}{{\text{R}}_{\text{1}}}\text{+}{{\text{R}}_{\text{2}}}\text{+}{{\text{R}}_{\text{3}}}$
From this equation, we can conclude that overall resistance increases when the resistors are connected in series.

To find the equivalent resistance of three resistors connected in parallel, we can use the equation given below.
$\dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}$
From the question, we can assign the resistance of each resistor as,

& {{R}_{1}}=2\Omega \\\ & {{R}_{2}}=3\Omega \\\ & {{R}_{3}}=6\Omega \\\ \end{aligned}$$ So, the equivalent resistance will be equal to, $$\dfrac{1}{R}=\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}$$ $$\dfrac{1}{R}=\dfrac{6}{6}$$ So, the equivalent resistance of three resistors are, $$R=1\Omega $$ Additional information: In a series connection of resistors, the current flowing through each resistor is the same. The total voltage is the sum of the voltage drops across each resistor. Drawbacks of a series circuit are; 1\. Short circuit will happen due to the overflow of current 2\. A high flow of current cause the damages to the equipment 3\. Every device has to turn off to switch off one device. These are the reasons for the preference of the parallel circuits for house wiring purposes. Note: In the series connection, the current will be the same and the total voltage will be the sum of voltages consumed by each resistor. So, we can find equivalent resistance by using this equation. $$\text{V=I}{{\text{R}}_{\text{1}}}\text{+I}{{\text{R}}_{\text{2}}}\text{+I}{{\text{R}}_{\text{3}}}$$ In a parallel connection, the voltage will be the same and the current will split up to each resistor. So, we can find equivalent resistance by using this equation. $$I=\dfrac{V}{{{R}_{1}}}+\dfrac{V}{{{R}_{2}}}+\dfrac{V}{{{R}_{3}}}$$