Question

Establish a relation between electric current and drift velocity. OR prove that the current density of metallic conductors is directly proportional to the drift speed of electrons.

Answer 1

Hint Here, we know that the concept of electric current and drift velocity so that we can analyze the electron w velocity should understand that current density J is a vector quantity defined as the current flowing per unit area measured in a normal direction to the charge flow direction.
Useful formula:
Current density,
$J = pv$
Where,
$J$ is electric current density,
$p$ charge the velocity,
$v$ velocity of density,

Complete step by step procedure
Relation between electric current and drift velocity.
Consider a uniform metallic wire $XY$ of length $1$ and cross-sectional area $A$. A potential difference V is applied across the ends $X$ and $Y$ of the wire.
At each point of the force wire, this causes an electric field.
$E = \dfrac{V}{l}........\left( i \right)$
This causes an electric field at each point of the force wire,${V_d}$ The opposite of the electric field's direction.
Current in wire $I = \dfrac{q}{t}..........\left( i \right)$
The distance traversed by each electron in time t = average\,velocity$$$X$ time = {V_d}t The total charge flowing in time $t$is equal to the total charge on the electrons present within the cylinder if we consider two planes $P$ and $Q$ at a distance ${V_d}$ in a conductor. 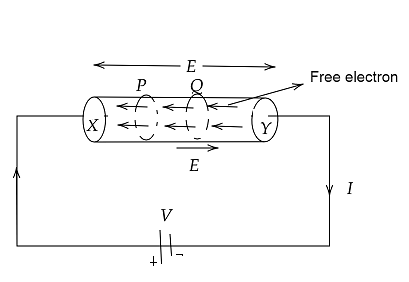The volume of this cylinder is equal to cross sectional area $X$ height $A{V_d}t$ If $n$ The number of free electrons per unit volume in the wire is then equal to the number of free electrons in the cylinder to $nA{V_d}t$  then, the total charge flowing through a cross section of the wire. q = \left( {nA{V_d}t} \right)\left( { - e} \right) = - neA{V_d}t.........\left( {iii} \right)$Therefore, Current flowing in the wire,$I = tq = t - v$​$;currentI = - neA{V_d}.......\left( {iv} \right)$This is the relation between current and drift velocity. Negative sign shows that the direction of current is opposite to the drift velocity$Numericaly;I = - neA\tau d...............\left( v \right)$Therefore, Current density,$J = \dfrac{l}{A}.$Rearranging the equation, We get,$ \Rightarrow JAI = d$Here, We get,$ \Rightarrow J\alpha D$$
Hence,
This is the metallic conductor's current density that is directly proportional to the drift velocity.

Note According to that a drift velocity is the average velocity obtained by charged particles in a medium due to an electrical field, such as electrons. In general, at Fermi velocity, an electron in a conductor will spread spontaneously, leading to an average velocity of zero.