Question
Question: Equivalent resistance between points A and B is A. \(3\,\Omega \) B. \(6\,\Omega \) C. \(1.5\,...
Equivalent resistance between points A and B is
A. 3Ω
B. 6Ω
C. 1.5Ω
D. 4.5Ω
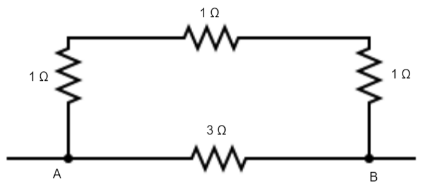
Solution
Equivalent resistance between two points can be evaluated after simplifying the circuit into simple series parallel combinations of resistors and then applying the appropriate formula. We will first identify which resistors are in series and which are in parallel and then apply suitable formulas. Since the equivalent resistance is asked between points A and B, we shall keep these as reference.
Formula used:
When the resistors are connected in series their equivalent is given by Rs=R1+R2........+Rn . When the resistors are connected in parallel, the equivalent resistance is given by Rp1=R11+R21+.........+Rn1 .
Complete step by step answer:
A series connection is identified to be the connection where the resistors are connected in a chain like fashion whereas in a parallel connection the resistors have the same starting and ending points in the circuit. In the given circuit, the 1Ω resistors are in series and their series combination is in parallel with the 3Ω resistor.
Using the formula for the series connection of resistors,
Rs=R1+R2........+Rn
Here we have three resistors so this formula reduces to Rs=R1+R2+R3.
Substituting the values we get,
Rs=1+1+1
⇒Rs=3Ω
Now the circuit is simplified as a parallel combination of two 3Ω resistors.
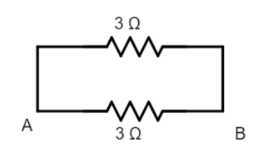
Using the formula for the parallel connection of resistors,
Rp1=R11+R21+.........+Rn1
Here we have two resistors so this formula reduces to Rp1=R11+R21
Substituting the values we get,
Rp1=31+31
⇒Rp1=32
∴Rp=23Ω which is the same as 1.5Ω
Hence, option C is the correct answer.
Note: We must carefully analyze the circuit for the series and parallel combinations. Sometimes it might happen due to the diagrammatic representation, we may perceive a wrong combination. Always remember that in a series combination, there is a voltage drop across all the resistors and the current remains the same. However, if the current gets distributed and there is no potential drop then it is a parallel combination.
