Question

Equivalent resistance between point x and y in the combination of resistance shown is

(A) $20\Omega$
(B) $18\Omega$
(C) $32\Omega$
(D) $40\Omega$

Answer 1

Hint
To solve this we need to first draw the circuit in a simplified way. Then we need to find the equivalent of the small parallel connection between $100\Omega$ and $25\Omega$. Then the equivalent in series with $100\Omega$ and the parallel $120\Omega$. Finally by finding the equivalent for the series connection with $100\Omega$ and parallel with $40\Omega$ we get the result.
In this solution, we will be using the following formula,
$\Rightarrow {R_{eq}} = {R_1} + {R_2} + {R_3} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in series.
and $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in a parallel circuit.

Complete step by step answer
To find the equivalent resistance, we first need to draw the simplified circuit. So we can draw the circuit as follows.

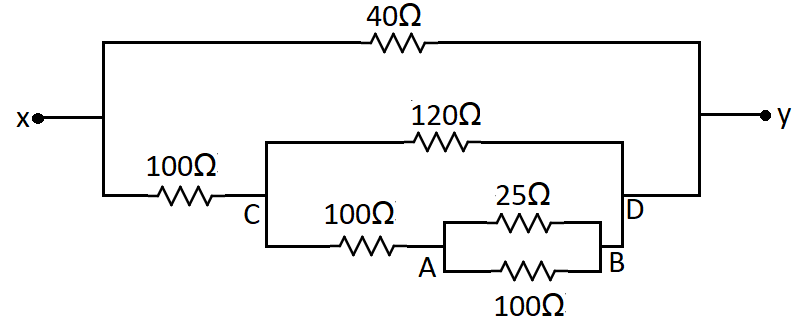
So first we need to find the equivalent resistance between A and B. Then using that value we need to find the equivalent resistance between points C and D. And then we can finally calculate the resistance between x and y.
So between points we have 2 resistances in parallel. So we use the formula,
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$
Where we substitute, ${R_1} = 100\Omega$ and ${R_2} = 25\Omega$. Hence we get,
$\Rightarrow \dfrac{1}{{{R_{eq1}}}} = \dfrac{1}{{100}} + \dfrac{1}{{25}}$
We take the LCM as 100. So we get
$\Rightarrow \dfrac{1}{{{R_{eq1}}}} = \dfrac{{1 + 4}}{{100}}$
On taking the reciprocal we get,
$\Rightarrow {R_{eq1}} = \dfrac{{100}}{5} = 20\Omega$
So this resistance is in series with $100\Omega$ in the bottom wire between the points C and D.
So we get the equivalent resistance in the bottom wire of CD as,
$\Rightarrow {R_{eq2}} = {R_1} + {R_2}$
We substitute, ${R_1} = 100\Omega$ and ${R_2} = {R_{eq1}} = 20\Omega$
So we get,
$\Rightarrow {R_{eq2}} = \left( {100 + 20} \right)\Omega$
On doing the addition we get the equivalent resistance as,
$\Rightarrow {R_{eq2}} = 120\Omega$
Therefore in between the points C and D there are 2 resistances in parallel. So to find the equivalent resistance between C and D we find the equivalent of the 2 resistances by,
$\Rightarrow \dfrac{1}{{{R_{eq3}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ where we substitute ${R_1} = 120\Omega$ and ${R_2} = 120\Omega$
So we get, $\dfrac{1}{{{R_{eq3}}}} = \dfrac{1}{{120}} + \dfrac{1}{{120}}$
By taking the LCM as 120, we get,
$\Rightarrow \dfrac{1}{{{R_{eq3}}}} = \dfrac{{1 + 1}}{{120}}$
We take the reciprocal and get the equivalent resistance as,
$\Rightarrow \dfrac{1}{{{R_{eq3}}}} = \dfrac{{1 + 1}}{{120}}{R_{eq3}} = \dfrac{{120}}{2} = 60\Omega$
Now this resistance is in series in the bottom wire between x and y. So we get the equivalent as,
$\Rightarrow {R_{eq4}} = {R_1} + {R_2}$ where ${R_1} = 100\Omega$ and ${R_2} = 60\Omega$
So we get, ${R_{eq4}} = 100 + 60 = 160\Omega$
This is the resistance in the bottom wire and in the top wire the resistance is $40\Omega$. So to get the equivalent resistance between x and y we calculate the equivalent resistance of these 2 parallel resistances as,
$\Rightarrow \dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ where ${R_1} = 160\Omega$ and ${R_2} = 40\Omega$
So we get,
$\Rightarrow \dfrac{1}{R} = \dfrac{1}{{160}} + \dfrac{1}{{40}}$
On taking LCM as 160 we get,
$\Rightarrow \dfrac{1}{R} = \dfrac{{1 + 4}}{{160}}$
So to get $R$ we take the reciprocal on both sides as,
$\Rightarrow R = \dfrac{{160}}{5} = 32\Omega$
Therefore, the equivalent resistance between points x and y is $32\Omega$.
Hence the correct answer is option (C).

Note
The equivalent resistance of any circuit is the aggregate of all the resistances connected in series or parallel between 2 points in a circuit. For resistances in series the current flow in them are equal but in case of parallel resistances, the current flow is different and depends on the value of the resistance.