Question

Equations of the diagonals of a rectangle are $y+8x-17=0$ and $y-8x+7=0$. If the area of the rectangle is 8 sq. units, then the equation of the sides of the rectangle is/are
A) x = 1
B) x + y = 1
C) y = 9
D) x – 2y = 3

Answer 1

Hint: Find equation of bisectors of diagonals of the rectangle. Find angle between both the lines (diagonals) by using relation $\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$where ${{m}_{1}}\And {{m}_{2}}$ are slopes of lines.

Here equations of both the diagonals of rectangle are
$y+8x-17=0$............................(1)
$y-8x+7=0$...........................(2)
We have to determine the sides of the rectangle if the area of the rectangle is 8. So, let us draw rectangle ABCD with bisectors of diagonals as below;

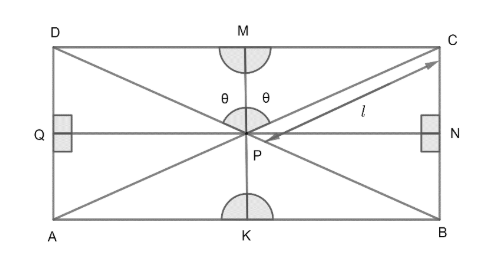
As, by the symmetry $\angle DPM=CPM\And \angle CPN=\angle BPN$ and area of all four triangles
$\Delta PCB=\Delta PBA=\Delta PAD=\Delta DPC$all will be equal.
We can prove the above relation as
$\text{ area of }\Delta PCD=\dfrac{1}{2}\times PM\times CD=\dfrac{1}{2}\times \dfrac{1}{2}KM\times CD$
Where KM = 2PM & KM = BC
Hence, $\text{ area of }\Delta PCD=\dfrac{1}{4}BC.CD$
Similarly, the area of all four triangles will be $\dfrac{1}{4}BC.CD$.
Therefore area of $\Delta DPC=\dfrac{1}{4}.area\text{ }of\text{ }rectangle$
As, we have area of rectangle as 8;
So, Area of $\Delta DPC=2$
Let us suppose $\angle DPM=\angle MPC=\theta$ and $CP='\ell '$.
Hence, from $\Delta MPC$, we can write
$\begin{aligned} & \sin \theta =\dfrac{MC}{PC}\text{ or }MC=\ell \sin \theta \\\ & \text{and }\cos \theta =\dfrac{MP}{CP}\text{ or }MP=\ell \cos \theta \\\ \end{aligned}$
Therefore,
$\begin{aligned} & \text{ area of }\Delta PCD=\dfrac{1}{2}\times CD\times MP \\\ & =\dfrac{1}{2}\times 2MC\times MP=\ell \sin \theta .\ell \cos \theta \\\ & ={{\ell }^{2}}\sin \theta \cos \theta \\\ \end{aligned}$
As, we already have area of $\Delta DPC=2,$ Hence we get;
${{\ell }^{2}}\sin \theta \cos \theta =2..............\left( 3 \right)$
Now, we know the equation of diagonals as well. As angles between them is $2\theta ,$ hence, we can use the relation
$\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$between two lines, where $\theta$ is angle between them and ${{m}_{1}}\text{ and }{{m}_{2}}$are slopes of them.
As, here angle is $2\theta$between two diagonals, and slopes can be determined by equations (1) and (2), so,
${{m}_{1}}=-8,{{m}_{2}}=8$
Therefore,
$\tan 2\theta =\left| \dfrac{-8-8}{1+\left( -8 \right)\left( 8 \right)} \right|=\dfrac{16}{63}$
Now, we can draw a triangle as

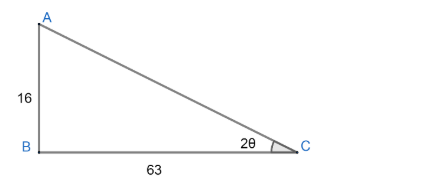
Where $AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}$ by Pythagoras theorem,
$\begin{aligned} & AC=\sqrt{{{16}^{2}}+{{63}^{2}}} \\\ & AC=\sqrt{256+3969} \\\ & AC=\sqrt{4225} \\\ & AC=65 \\\ \end{aligned}$
Hence, from the given triangle, we get
$\cos 2\theta =\dfrac{63}{65},\sin 2\theta =\dfrac{16}{65}........................\left( 4 \right)$
Now, from equation (3), we have
${{\ell }^{2}}\sin \theta \cos \theta =2$
Multiplying both sides by 2, we get
${{\ell }^{2}}\left( 2\sin \theta \cos \theta \right)=4$
We know that $\sin 2\theta =2\sin \theta \cos \theta$, hence above equation can be written as;
${{\ell }^{2}}\sin 2\theta =4$
From equation (4), we have ,
$\begin{aligned} & \sin 2\theta =\dfrac{16}{65},\text{hence} \\\ & {{\ell }^{2}}\times \dfrac{16}{65}=4 \\\ & {{\ell }^{2}}=\dfrac{65}{4}\text{ or }\ell =\dfrac{\sqrt{65}}{2}.................\left( 5 \right) \\\ \end{aligned}$
Now, we can calculate length PM and PN from $\Delta PMC$.
As,
$\begin{aligned} & MC=\ell \sin \theta \\\ & PM=\ell \cos \theta \\\ \end{aligned}$
Now, we have $\cos 2\theta \And \sin 2\theta$ from equation (4), Hence, we need to convert $\sin \theta \And \cos \theta$ in following way;
We know a trigonometric identity as;
$\cos 2\theta =2{{\cos }^{2}}\theta -1=1-2{{\sin }^{2}}\theta$
Hence, we can rewrite the above identity as
$\begin{aligned} & {{\cos }^{2}}\theta =\dfrac{1+{{\cos }^{2}}\theta }{2},{{\sin }^{2}}\theta =\dfrac{1-\cos 2\theta }{2} \\\ & Or \\\ & \cos \theta =\sqrt{\dfrac{1+\cos 2\theta }{2}}, \\\ & sin\theta =\sqrt{\dfrac{1-\cos 2\theta }{2}} \\\ \end{aligned}$
Now, we can get MC and PM as
$\begin{aligned} & MC=\ell \sqrt{\dfrac{1-\cos 2\theta }{2}} \\\ & and \\\ & PM=\ell \sqrt{\dfrac{1+\cos 2\theta }{2}} \\\ \end{aligned}$
We know $\cos 2\theta =\dfrac{63}{65}$ from equation (4),
Hence,
$\begin{aligned} & MC=\ell \sqrt{\dfrac{1-\dfrac{63}{65}}{2}}=\ell \sqrt{\dfrac{2}{65}\times }\dfrac{1}{2} \\\ & MC=\dfrac{\ell }{\sqrt{65}} \\\ & and \\\ & PM=\ell \sqrt{\dfrac{1+\dfrac{63}{65}}{2}}=\ell \sqrt{\dfrac{128}{65}\times \dfrac{1}{2}} \\\ & PM=\ell \sqrt{\dfrac{64}{65}}=\dfrac{8\ell }{\sqrt{65}} \\\ \end{aligned}$
Now, we have already calculated the value of $\ell$, from equation (5). Hence,
$\begin{aligned} & PM=\dfrac{8}{\sqrt{65}}\times \dfrac{\sqrt{65}}{2}=4 \\\ & MC=\dfrac{1}{\sqrt{65}}\times \dfrac{\sqrt{65}}{2}=\dfrac{1}{2} \\\ \end{aligned}$
Therefore,
$PM=4\text{ and }MC=\dfrac{1}{2}...................\left( 6 \right)$
Now, we know that if two lines$ax+by+c=0\text{ and }{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0$ are given, then their bisector are given by relation;
$\dfrac{ax+by+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=\pm \dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{\sqrt{{{a}_{1}}^{2}+{{b}_{1}}^{2}}}..........\left( 7 \right)$
Now, from the given rectangle ABCD, MK and NQ are the bisector of diagonals BD and AC. Hence, we can write equation of MK and NQ by using equation (7) as;
We have diagonals BD and AC from equation (1) and (2) be
$\begin{aligned} & y+8x-17=0\text{ and }y-8x+7=0 \\\ & or \\\ & 8x+y-17=0\text{ and }8x-y-7=0 \\\ \end{aligned}$
Hence, using equation (7) we get equations of bisectors as;
$\begin{aligned} & \dfrac{8x+y-17}{\sqrt{{{1}^{2}}+{{8}^{2}}}}=\pm \dfrac{8x-y-7}{\sqrt{{{1}^{2}}+{{8}^{2}}}} \\\ & Or \\\ & 8x+y-17=\pm \left( 8x-y-7 \right) \\\ \end{aligned}$
Case 1: Taking ‘+’ sign from another side of equal to, we get
$\begin{aligned} & 8x+y-17=8x-y-7 \\\ & 2y=10 \\\ & y=5..............\left( 8 \right) \\\ \end{aligned}$
Case 2: Taking ‘-’ sign from another side of equals to , we get,

& 8x+y-17=-8x+y+7 \\\ & 16x=24 \\\ & x=\dfrac{24}{16}=\dfrac{3}{2} \\\ & x=\dfrac{3}{2}....................\left( 9 \right) \\\ \end{aligned}$$ Now, as we already know that the MK bisector is parallel to AD and BC and the NQ bisector is parallel to AB and CD. Therefore, we have equations y = 5 and $x=\dfrac{3}{2}$ of the bisectors MK and QN and we know the distance PQ, PN, PM and PK as well. Case 1: If KM is representing y = 5 and QN is representing $x=\dfrac{3}{2}$. Then, AD and BC is given as $y=5\pm \left( PN\text{ or }QP \right)$ We have $$MC=PN=QP=\dfrac{1}{2}$$ from equation (6). Hence, $$\begin{aligned} & y=5\pm \dfrac{1}{2}=\dfrac{11}{2}\text{ and }\dfrac{9}{2} \\\ & y=\dfrac{11}{2}\text{ and }y=\dfrac{9}{2} \\\ \end{aligned}$$ Similarly, CD and AB are given as $\begin{aligned} & x=\dfrac{3}{2}\pm 4=\dfrac{11}{2}\text{ and }\dfrac{-5}{2} \\\ & x=\dfrac{-5}{2}\text{ and }x=\dfrac{11}{2} \\\ \end{aligned}$ Hence, equations of sides of rectangle are $x=\dfrac{-5}{2},x=\dfrac{11}{2}\text{ and }y=\dfrac{9}{2},\dfrac{11}{2}$ Case 2 : If KM is representing $x=\dfrac{3}{2}$ and QN is representing y = 5 AD and BC are given as; $\begin{aligned} & x=\dfrac{3}{2}\pm \dfrac{1}{2}=2,1 \\\ & x=1\And x=2 \\\ \end{aligned}$ CD and AB are given as $\begin{aligned} & y=5\pm 4=1,9 \\\ & y=1\And y=9 \\\ \end{aligned}$ Hence, equation of sides of rectangle are; X = 1, x = 2, and y = 1, y = 9 So, option A and C are the answer. Note: Another approach for this question would be to suppose four sides of rectangle i.e. AB, BC, CD and AD as $\begin{aligned} & y=mx+c \\\ & y=\dfrac{-1}{m}x+{{c}_{1}} \\\ & y=mx+{{c}_{2}} \\\ & y=\dfrac{-1}{m}x+{{c}_{3}} \\\ \end{aligned}$ Now, calculate distances between sides and equate area to 8. Now, find the intersection of the above equation to get A, B, C, D. Now, put the points A, B, C, D to given diagonals BD and AC to get four equations. Now, we will have five equations and five variables from the above conditions. Solving the equations takes longer than the given solution. One can get confused by the two cases explained in solutions. So there is a possibility of two rectangles according to the information. That’s why we have got 8 equations of lines 4 pairs representing one rectangle and 4 are representing others.