Question

Equation of the line of the shortest distance between the lines $\dfrac{x}{1} = \dfrac{y}{{ - 1}} = \dfrac{z}{1}$ and $\dfrac{{x - 1}}{0} = \dfrac{{y + 1}}{{ - 2}} = \dfrac{z}{1}$ is
A) $\dfrac{x}{1} = \dfrac{y}{{ - 1}} = \dfrac{z}{2}$
B) $\dfrac{{x - 1}}{1} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{{ - 2}}$
C) $\dfrac{{x - 1}}{1} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{1}$
D) $\dfrac{x}{{ - 2}} = \dfrac{y}{1} = \dfrac{z}{2}$

Answer 1

A equation of a line can be written if we know a point that lies on the line and the direction of the line.
Let a point $\left( {{x_1},{y_1},{z_1}} \right)$ , lie on the line, and have direction ratios: $\left( {a,b,c} \right)$
Cartesian equation of the line:
$\dfrac{{x - {x_1}}}{a} = \dfrac{{y - {y_1}}}{b} = \dfrac{{z - {z_1}}}{c}$
Vector equation of the line:
$x\hat i + y\hat j + z\hat k = \left( {{x_1}\hat i + {y_1}\hat j + {z_1}\hat k} \right) + \lambda \left( {a\hat i + b\hat j + c\hat k} \right)$
$\vec r = x\hat i + y\hat j + z\hat k$ , ${\vec a_1} = {x_1}\hat i + {y_1}\hat j + {z_1}\hat k$ , ${\vec b_1} = a\hat i + b\hat j + c\hat k$
Therefore, the vector equation of a line:
${\vec r} = {\vec a_1} + \lambda {\vec b_1}$
Cross product (or vector product) of two nonzero vectors $\vec a$ and $\vec b$ is the product of the magnitude of both vectors $\vec a$ and $\vec b$, and sine of the angle between them. i.e.
$\hat a \times \hat b = \left| {\hat a} \right|\left| {\hat b} \right|\sin \theta {\text{ }}\hat n$, where $\theta$ is the acute angle between vectors $\vec a$ and $\vec b$. Here $\hat n$ is the unit vector perpendicular to the plane containing vectors $\vec a$ and $\vec b$. The resultant vector is perpendicular to both vectors $\vec a$ and $\vec b$.

Complete step-by-step answer:
Step 1: Illustration of the given question:

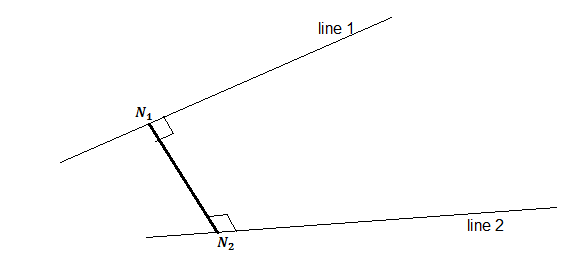
Let ${N_1}$ be any arbitrary point lie on line 1
Equation of line 1: $\dfrac{x}{1} = \dfrac{y}{{ - 1}} = \dfrac{z}{1}$
On comparing with the standard Cartesian equation of the line: $\dfrac{{x - {x_1}}}{a} = \dfrac{{y - {y_1}}}{b} = \dfrac{{z - {z_1}}}{c}$
Direction ratios of line 1: $\left( {1, - 1,1} \right)$
Vector equation of line 1: ${\vec r_1} = \lambda \left( {\hat i - \hat j + \hat k} \right)$
Thus, an arbitrary point on a line is given by $\left( {x,y,z} \right)$ :
$x = \lambda ;{\text{ }}y = - \lambda ;{\text{ }}z = \lambda$
Therefore, coordinates of ${N_1} = \left( {\lambda , - \lambda ,\lambda } \right)$
Let ${N_2}$be any arbitrary point lie on line 2
Equation of line 2: $\dfrac{{x - 1}}{0} = \dfrac{{y + 1}}{{ - 2}} = \dfrac{z}{1}$
On comparing with the standard Cartesian equation of the line: $\dfrac{{x - {x_1}}}{a} = \dfrac{{y - {y_1}}}{b} = \dfrac{{z - {z_1}}}{c}$
Direction ratios of line 2: $\left( {0, - 2,1} \right)$
Vector equation of line 2: ${\vec r_2} = \left( {\hat i - \hat j} \right) + \mu \left( { - 2\hat j + \hat k} \right)$
Thus, an arbitrary point on a line is given by $\left( {x,y,z} \right)$ :
$x = 1;{\text{ }}y = - 1 - 2\mu ;{\text{ }}z = \mu$
Therefore, coordinates of ${N_2} = \left( {1, - 1 - 2\mu ,\mu } \right)$
Step 2: Find direction ratios of line joining points ${N_2}$and ${N_1}$
Let the distance ${N_2}{N_1}$ be the smallest. Therefore the line joining points ${N_2}$ and ${N_1}$is the equation of the line of having the smallest distance between given lines.
Therefore, the vector $\overrightarrow {{N_2}{N_1}}$ is a line joining the points ${N_2}$ and ${N_1}$
We know that the shortest distance is the line which is perpendicular to both the given lines.
Hence, $\overrightarrow {{N_2}{N_1}}$ the vector is perpendicular to both given lines.
$\Rightarrow \overrightarrow {{N_2}{N_1}} = k\left( {{{\vec b}_1} \times {{\vec b}_2}} \right)$
Here, the vector ${\vec b_1}$ is the direction ratio of line 1, and the vector ${\vec b_2}$ is the direction ratio of line 2.
\Rightarrow k\left| {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k} \\\ 1&{ - 1}&1 \\\ 0&{ - 2}&1 \end{array}} \right|
$\Rightarrow k\left[ {\hat i\left( { - 1 + 2} \right) - \hat j\left( {1 - 0} \right) + \hat k\left( { - 2 - 0} \right)} \right] \\\ \Rightarrow \overrightarrow {{N_2}{N_1}} = k\hat i - k\hat j - 2k\hat k \\\$
Hence, its direction ratios are: $\left( {k, - k, - 2k} \right)$ …… (1)
Also, the direction ratio of the line if two points on the line are given, is:
Let's say points $\left( {{x_1},{y_1},{z_1}} \right)$ and $\left( {{x_2},{y_2},{z_2}} \right)$ lie on one line.
Hence, direction ratios of the line is given by: $\left( {{x_2} - {x_1},{y_2} - {y_1},{z_2} - {z_1}} \right)$
Therefore, direction ratios of the line joining points ${N_2}$and ${N_1}$is: $\left( {1 - \lambda , - 1 - 2\mu + \lambda ,\mu - \lambda } \right)$ ……(2)
Step 3: Find the coordinates of points ${N_2}$and ${N_1}$.
Direction ratios of the line joining points ${N_2}$and ${N_1}$obtained in equation (1) and (2) will be equal to each other as they are of the same line.
Hence from equation (1) and (2), we can write:
$1 - \lambda = k$ …… (3)
$- 1 - 2\mu + \lambda = - k$ ……(4)
$\mu - \lambda = - 2k$ …… (5)
Adding (3) and (4)
$\- 2\mu = 0 \\\ \Rightarrow \mu = 0 \\\$
Put $\mu = 0$ in equation (5)
$0 - \lambda = - 2k \\\ \Rightarrow \lambda = 2k \\\$
Put $\lambda = 2k$ in equation (3)
$1 - 2k = k \\\ \Rightarrow 1 = 3k \\\ \Rightarrow k = \dfrac{2}{3} \\\$
$\lambda = 2k \\\ \because \lambda = \dfrac{2}{3} \\\$
Therefore, the coordinates of the ${N_1} = \left( {\lambda , - \lambda ,\lambda } \right) = \left( {\dfrac{2}{3}, - \dfrac{2}{3},\dfrac{2}{3}} \right)$
Therefore, coordinates of the ${N_2} = \left( {1, - 1 - 2\mu ,\mu } \right) = \left( {1, - 1,0} \right)$
Step 4: Find the equation of the required line.
Equation of the line if two points on the line are given, is:
Let's say points $\left( {{x_1},{y_1},{z_1}} \right)$ and $\left( {{x_2},{y_2},{z_2}} \right)$ lie on one line.
Hence, the Cartesian equation of the line: $\dfrac{{x - {x_2}}}{{{x_2} - {x_1}}} = \dfrac{{y - {y_2}}}{{{y_2} - {y_1}}} = \dfrac{{z - {z_2}}}{{{z_2} - {z_1}}}$
Therefore, the Cartesian equation of the line joining points ${N_2}$and ${N_1}$is: $\dfrac{{x - 1}}{{1 - \dfrac{2}{3}}} = \dfrac{{y + 1}}{{ - 1 + \dfrac{2}{3}}} = \dfrac{z}{{0 - \dfrac{2}{3}}}$
$\Rightarrow \dfrac{{x - 1}}{{\dfrac{1}{3}}} = \dfrac{{y + 1}}{{ - \dfrac{1}{3}}} = \dfrac{z}{{ - \dfrac{2}{3}}}$
3 is common is to each
Therefore, $\dfrac{{x - 1}}{1} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{{ - 2}}$
Final answer: The equation of the line of the shortest distance is $\dfrac{{x - 1}}{1} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{{ - 2}}$ .

Thus, the correct option is (B).

Note: Dot product (or scalar product) between two non-zero vectors $\vec a$ and $\vec b$ is the product of the magnitude of each vector and cosine of the angle between them:
$\vec a \cdot \vec b = \left| a \right|\left| b \right|\cos \theta$ , where $\theta$ is the acute angle between vectors $\vec a$ and $\vec b$.
If the direction ratios of the required line are not in proportion with an option equation of the line . This means that option is incorrect.
If the direction ratios of the required line are in proportion with an option equation of the line. Then that option may or may not be correct. Check if the point lying on the option line satisfies the equation of the required line or not.
Vector $\overrightarrow {{N_2}{N_1}}$ will be parallel to the direction of $\left( {{{\vec b}_1} \times {{\vec b}_2}} \right)$, may or may not be exactly in direction of $\left( {{{\vec b}_1} \times {{\vec b}_2}} \right)$. Hence, $\overrightarrow {{N_2}{N_1}} = k\left( {{{\vec b}_1} \times {{\vec b}_2}} \right)$.