Question

Equation of tangent to the Ellipse $2{x^2} + {y^2} = 8$ makes an angle ${45^ \circ }$ with x-axis.

Answer 1

First, we will find the slope of the tangent by two ways. First we will find $\dfrac{{dy}}{{dx}}$ by differentiating the equation of given Ellipse $2{x^2} + {y^2} = 8$ . Then we will find the $\dfrac{{dy}}{{dx}}$ by equating it to $\tan \theta$ , where $\theta$ would be $45^\circ$. Then we will use these two equations to find x,y. Hence we would get a point which lies on the required equation of tangent. Then we would put these points in the general equation of a tangent to a Ellipse.

Complete step by step solution:
According to the question the equation of the Ellipse is
$2{x^2} + {y^2} = 8$ … (1)
Hence, the diagram for the question must look like

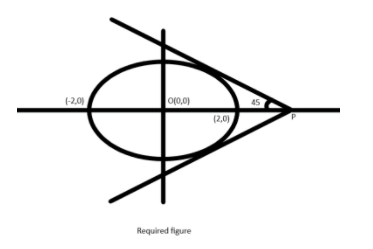
We know that tangent to the Ellipse whose equation is given to us can be calculated by differentiating the given equation of the Ellipse, that is

Differentiating (1) with respect to x, we get the slope of the tangent to the Ellipse at $(x,y)$ as
$\Rightarrow \dfrac{{d(2{x^2} + {y^2})}}{{dx}} = \dfrac{d}{{dx}}(8)$

Using distributive property of derivatives, we get
$\Rightarrow \dfrac{{d(2{x^2})}}{{dx}} + \dfrac{{d{y^2}}}{{dx}} = \dfrac{d}{{dx}}(8)$
Using $\dfrac{{d(ay)}}{{dx}} = a \times \dfrac{{dy}}{{dx}}$ , we get
$\Rightarrow 2\dfrac{{d{x^2}}}{{dx}} + \dfrac{{d{y^2}}}{{dx}} = \dfrac{d}{{dx}}(8)$

Using $\dfrac{{df{{(x)}^n}}}{{dx}} = n \times f{(x)^{n - 1}} \times \dfrac{{df(x)}}{{dx}}$ , we get
$\Rightarrow 4x\dfrac{{dx}}{{dx}} + 2y\dfrac{{dy}}{{dx}} = \dfrac{d}{{dx}}(8)$
Using $\dfrac{{da}}{{dx}} = 0$ , when a is a constant, we get
$\Rightarrow 4x + 2y\dfrac{{dy}}{{dx}} = 0$
Taking 4x to RHS, we get
$\Rightarrow 2y\dfrac{{dy}}{{dx}} = - 4x$
Taking all the terms to RHS except $\dfrac{{dy}}{{dx}}$ , we get
$\Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{ - 4x}}{{2y}}$ +
Hence,
$\Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{ - 2x}}{y}$
We know that ,
$\dfrac{{dy}}{{dx}} = m = \tan \theta$

Where m is the slope of the tangent to the Ellipse at $(x,y)$ , Hence
$\Rightarrow \tan \theta = \dfrac{{ - 2x}}{y}$

According to the question, $\theta = 45^\circ$ , Hence
$\Rightarrow \tan 45^\circ = \dfrac{{ - 2x}}{y}$
Put, $\tan 45^\circ = 1$ in the above equation, we get
$\Rightarrow 1 = \dfrac{{ - 2x}}{y}$
On multiplying the equation by y we get,
$\Rightarrow y = - 2x$ … (2)
Put $y = - 2x$ in (1), we get
$\Rightarrow 2{x^2} + {( - 2x)^2} = 8$
On simplification we get,
$\Rightarrow 2{x^2} + 4{x^2} = 8$
On adding like terms we get,
$\Rightarrow 6{x^2} = 8$
On dividing the equation by 6 we get,
$\Rightarrow {x^2} = \dfrac{8}{6}$
On simplification we get,
$\Rightarrow {x^2} = \dfrac{4}{3}$
Taking square root on both sides of the equation, we get
$\Rightarrow x = \sqrt {\dfrac{4}{3}}$
On simplification we get,
$\Rightarrow x = \dfrac{2}{{\sqrt 3 }}$ … (3)

Now, put $x = \dfrac{2}{{\sqrt 3 }}$ in (2), we get
$\Rightarrow y = - 2 \times \dfrac{2}{{\sqrt 3 }}$
$\Rightarrow y = \dfrac{{ - 4}}{{\sqrt 3 }}$ ... (4)
We know that general equation of tangent for any curve is
$\Rightarrow (y - {y_1}) = \dfrac{{dy}}{{dx}}(x - {x_1})$
Now, on substituting $x = \dfrac{2}{{\sqrt 3 }}$ , $y = \dfrac{{ - 4}}{{\sqrt 3 }}$ and $\dfrac{{dy}}{{dx}} = \tan {45^ \circ } = 1$ , we get
$\Rightarrow (y - (\dfrac{{ - 4}}{{\sqrt 3 }}) = 1 \times (x - \dfrac{2}{{\sqrt 3 }})$
On simplification we get,
$\Rightarrow (y + \dfrac{4}{{\sqrt 3 }}) = (x - \dfrac{2}{{\sqrt 3 }})$
On taking LCM we get,
$\Rightarrow (\dfrac{{y\sqrt 3 }}{{\sqrt 3 }} + \dfrac{4}{{\sqrt 3 }}) = (\dfrac{{x\sqrt 3 }}{{\sqrt 3 }} - \dfrac{2}{{\sqrt 3 }})$
Multiplying through by $\sqrt 3$ , we get
$\Rightarrow y\sqrt 3 + 4 = x\sqrt 3 - 2$
On rearranging we get,
$\Rightarrow 6 = x\sqrt 3 - y\sqrt 3$
Hence we have,
$\Rightarrow x\sqrt 3 - y\sqrt 3 = 6$

Hence, $x\sqrt 3 - y\sqrt 3 = 6$ is the equation of tangent to the Ellipse $2{x^2} + {y^2} = 8$ making an angle ${45^ \circ }$ with x-axis.

Note:
We know that a tangent is a line which touches the Ellipse at only one point. In the above question we have found out that point. Hence to check ourselves and the answer, we can put that point in the equation of the Ellipse also, if it does not satisfy the given equation, our answer must be WRONG. And we should check our answers for mistakes immediately.