Question

Equation of line parallel to x-axis and 2 units above the origin is
$(a){\text{ x = 2}} \\\ (b){\text{ x = - 2}} \\\ (c){\text{ y = 2}} \\\ (d){\text{ y = - 2}} \\\$

Answer 1

Hint – In this question plot a graphical representation, start by identifying the x axis which a horizontal line is passing through the origin. Then move two units up that is the coordinate $(0,2)$and draw a straight line passing through this coordinate parallel to the previously identified x axis.
Complete step-by-step solution -

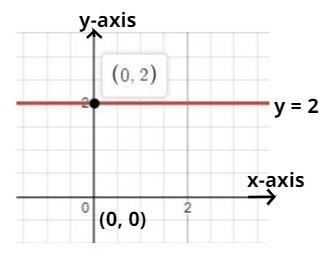
We have to write the equation of line parallel to x-axis and 2 – units above the origin.
As we know on the y-axis the value of x coordinates is zero.
So the coordinate 2 units above the origin is (x, y) = (0, 2)
Now as we know that the slope (m) of the line parallel to x-axis is zero.
$\Rightarrow m = 0.$
Now the equation of line passing through point (x1, y1) and slope m is
$\Rightarrow \left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$
Now substitute the values we have,
$\Rightarrow \left( {y - 2} \right) = 0\left( {x - 0} \right)$
$\Rightarrow y = 2$
Is the required equation of line parallel to the x-axis and 2 units above the origin as shown in figure.
So this is the required answer.

Note – Slope of any line is defined as the angle which the line makes with the positive direction of the x-axis in anticlockwise sense. So if we talk about the slope of the line which has the equation $y = 2$ then it will be ${0^0}$ because the line is parallel to the x-axis.