Question

Equation of chord AB of circle ${x^2} + {y^2} = 2\;$ passing through $P(2,2)$ such that $\dfrac{{PB}}{{PA}} = 3$ , is given by

Answer 1

We will assume a chord AB on the circle ${x^2} + {y^2} = 2\;$ which passes through point $P\left( {2,2} \right)$. Then we will take a chord $A^{‘}B^{‘}$ passing through the center and point $P\left( {2,2} \right)$. We will find PO (Distance from P to O using distance formula). Then we will find $PB^{‘}$ from the relationship $PB^{‘}=PO-OB^{‘}$. Then we divided PO by $PB^{‘}$ to compare this with the given relation $\dfrac{{PB}}{{PA}} = 3$ . After comparing the two equations, we would be able to say that chord AB and $A^{‘}B^{‘}$ are the same. Hence, diameter is the required chord. Now we know that the required chord passes through center $O\left( {0,0} \right)$ and point $P\left( {2,2} \right)$ . Hence, we can easily find the required equation using the two point form of the equation.

Complete step by step solution:
According to the question, we may assume the figure to be

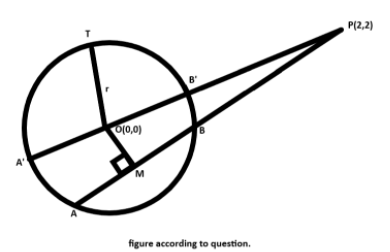
We know that $OA' = OB' = r$ …(1)
Where r is the radius of the given circle.
Given equation of the circle
${x^2} + {y^2} = \,\,2$ …(2)

We know that general equation of a circle is
${x^2} + {y^2} = \,\,{r^2}$ … (3)
Comparing (2)and (3), we get
$\Rightarrow {r^2} = 2$
On taking Square root we get,
$\Rightarrow r = \sqrt 2$ …(4)

We know that $A'B' = OA' + OB'$ is the diameter of the given circle
$\Rightarrow A'B' = 2\sqrt 2$ …(5)

From the figure , we get
$\Rightarrow PB' = PO - OB'$ …(6)

And we know the points $P(2,2)$ and $O\left( {0,0} \right)$ , we can find the distance by distance formula
$D = \sqrt {{{({x_1} - {x_2})}^2} + \,\,{{({y_1} - {y_2})}^2}}$
On substituting the values we get,
$\Rightarrow PO = \sqrt {{{(2 - 0)}^2} + \,\,{{(2 - 0)}^2}}$
Hence on simplification we get,
$\Rightarrow PO = \sqrt {4 + 4}$
On adding terms under the root we get,
$\Rightarrow PO = \sqrt 8$
On further simplification we get,
$\Rightarrow PO = 2\sqrt 2$ …(7)

Substituting the value of PO and $OB'$ in (6) from (7) and (1), we get
$\Rightarrow PB' = 2\sqrt 2 - \sqrt 2$
On simplification we get,
$\Rightarrow PB' = \sqrt 2$ …(8)

Now we can see that
$PA' = PB' + A'B'$

Substituting values of $PA' = PB' + A'B'$ from (5) and (8)
$\Rightarrow PA' = \sqrt 2 + 2\sqrt 2$
On simplification we get,
$\Rightarrow PA' = 3\sqrt 2$ …(9)

Also from (8) we get $PB' = \sqrt 2$

Now dividing (9) by (8), we get
$\Rightarrow \dfrac{{PA'}}{{PB'}} = \dfrac{{3\sqrt 2 }}{{\sqrt 2 }}$
On cancelling common terms we get,
$\Rightarrow \dfrac{{PA'}}{{PB'}} = 3$

And from the question we have
$\Rightarrow \dfrac{{PA}}{{PB}} = 3$
$\Rightarrow AB = A'B'$

Hence, diameter is the required chord and it passes through center $O\left( {0,0} \right)$ and $P\left( {2,2} \right)$ .

Hence, by using two point form of the equation, we get
$\dfrac{{y - {y_1}}}{{x - {x_1}}} = \dfrac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}}$
Where ${x_1} = 0\,,\,{x_2} = 2\,,\,{y_1} = 0\,,\,{y_2} = 2\,$

Hence,
$\Rightarrow \dfrac{{y - 0}}{{x - 0}} = \dfrac{{0 - 2}}{{0 - 2}}$
On simplification we get,
$\Rightarrow \dfrac{y}{x} = \dfrac{{ - 2}}{{ - 2}}$
On cancelling common terms we get,
$\Rightarrow \dfrac{y}{x} = 1$
On cross multiplication we get,
$\Rightarrow y = x$

**Hence , the required equation is
$\Rightarrow x = y$ **

Note:
When trying to solve these kind of equation based questions, each and every symbol in the general equation represents something for example in the equation of circle given in the question,
${x^2} + {y^2} = \,\,2$
$\sqrt 2$ is the radius, before even attempting these questions one should extract all the values represented by the equation in order to solve the question with ease.