Question

Equation of a straight line whose slope is $\dfrac{-1}{5}$ and y-intercept is ‘-6’ is $x+5y+30=0$.
(a) True
(b) False

Answer 1

Hint: Use the slope and intercept form of a straight line which is given as $y=mx+c$ where m is the slope of the line and c is the length of intercept on y-axis by the line. Now verify the equation of line by the given line.

Complete step-by-step answer:

Here it is given that slope of line is $\dfrac{-1}{5}$ and the intercept of the same line with x-axis is ‘-6’, so we need to verify the statement whether the equation of the line would be $x+5y+30=0$ or not or something else.
Let us try to find out the equation of the line with the information’s slope and intercept.
Now, we know that the general form of the equation of line is given as $ax+by+c=0$.
Here a, b, c are some constants. So, we cannot relate intercept or slope with this equation.
Hence, we need to use the slope and intercept form of the equation of the straight line. It is given by the relation $y=mx+c$, where m is the slope of the line and c is the y-intercept. Intercept means length cut by line on y-axis from origin as shown below.

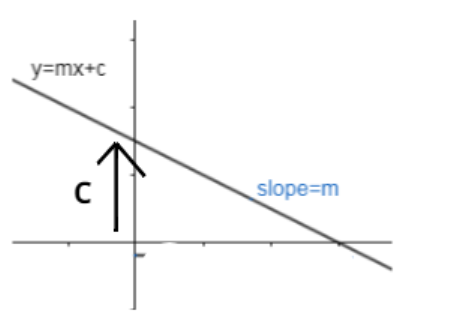
Now, we can put values of slope i.e. ’m’ and y-intercept i.e. ‘c’ from the given information in the problem.
Now, we know that slope is $\dfrac{-1}{5}$ and y-intercept is -6. So, values of m and c can be given as
$m=\dfrac{-1}{5}$
c = - 6
Now, we can put values of m and c in the slope intercept form of the line i.e., $y=mx+c$.
Hence we get,
$\begin{aligned} & y=\dfrac{-1}{5}x-6 \\\ & \Rightarrow y=\dfrac{-1}{5}x-\dfrac{6}{1} \\\ \end{aligned}$
Now, take LCM in the right hand side of the above equation. Hence we get
$\dfrac{y}{1}=\dfrac{-x-30}{5}$
On cross multiplying the above equation we get
$5y=-x-30$
Now transfer the terms $-x$ and ‘-30’ to the other side. Hence we get

& 5y+x+30=0 \\\ & \Rightarrow x+5y+30=0 \\\ \end{aligned}$$ Hence, the equation of the line i.e., $$x+5y+30=0$$ has slope as $\dfrac{-1}{5}$ and intercept -6. So, yes the given statement is true. Note: Another approach of the given question would be that we could convert the given equation of line to verify the given slope and intercept values. Hence, given equation of line is $\begin{aligned} & x+5y+30=0 \\\ & \Rightarrow 5y=-x-30 \\\ & y=\dfrac{-1}{5}x-6 \\\ \end{aligned}$ $m=\dfrac{-1}{5},c=-6$ One needs to be very clear with all the forms of straight lines. We can use only one form of equation of line in the whole chapter of straight line as well but using and knowing the different forms will always help to keep the solution in easier way. And we can solve the question very efficiently.