Solveeit Logo
Login

Question

Question: Equation $\frac{a^2}{x-\alpha}+\frac{b^2}{x-\beta}+\frac{c^2}{x-\gamma}=m-n^2x$ (a, b, c, m, n ∈ R) ...

Equation a2x−α+b2x−β+c2x−γ=m−n2x\frac{a^2}{x-\alpha}+\frac{b^2}{x-\beta}+\frac{c^2}{x-\gamma}=m-n^2x (a, b, c, m, n ∈ R) has necessarily

A

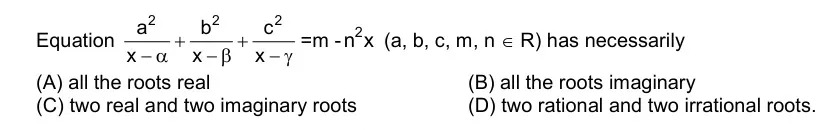
all the roots real

B

all the roots imaginary

C

two real and two imaginary roots

D

two rational and two irrational roots.

Answer

Option (C): Two real and two imaginary roots.

Explanation

Solution

Solution:

Write the equation:

a2x−α+b2x−β+c2x−γ=m−n2x.\frac{a^2}{x-\alpha}+\frac{b^2}{x-\beta}+\frac{c^2}{x-\gamma}=m-n^2x.

Assume that the parameters a,b,ca,b,c are nonzero, so that a2,b2,c2>0a^2,b^2,c^2>0, and that α,β,γ\alpha,\beta,\gamma are distinct real numbers. Clearing the denominators by multiplying both sides by

(x−α)(x−β)(x−γ)(x-\alpha)(x-\beta)(x-\gamma)

yields an equation

a2 (x−β)(x−γ)+b2 (x−α)(x−γ)+c2 (x−α)(x−β)=(m−n2x)(x−α)(x−β)(x−γ).a^2\,(x-\beta)(x-\gamma)+b^2\,(x-\alpha)(x-\gamma)+c^2\,(x-\alpha)(x-\beta)=\bigl(m-n^2x\bigr)(x-\alpha)(x-\beta)(x-\gamma).

The left‐side is a sum of three quadratics (degree 2 in xx) while the right‐side is the product of a linear term with a cubic so (in general) you obtain a quartic (4th degree) equation in xx.

Now, note that in the original equation the terms

a2x−α,b2x−β,c2x−γ\frac{a^2}{x-\alpha},\quad \frac{b^2}{x-\beta},\quad \frac{c^2}{x-\gamma}

have vertical asymptotes at x=α,β,γx=\alpha,\beta,\gamma (with the corresponding term blowing up to +∞+\infty from one side and to −∞-\infty from the other). Since the numerators a2,b2,c2a^2,b^2,c^2 are positive, the behavior of the function on the intervals determined by α,β,γ\alpha,\beta,\gamma is “forced” (the function jumps from +∞+\infty to −∞-\infty or vice‐versa in some of the intervals). In particular, in the intervals between the poles the equation

a2x−α+b2x−β+c2x−γ=m−n2x\frac{a^2}{x-\alpha}+\frac{b^2}{x-\beta}+\frac{c^2}{x-\gamma}=m-n^2x

has a change of sign by the Intermediate Value Theorem giving one real root in each of two consecutive intervals (say, between α\alpha and β\beta and between β\beta and γ\gamma).

The remaining two roots (since the cleared equation is a quartic) cannot be made to appear on the real axis by the structure of the left‐side (formed from sums of hyperbolic terms with fixed vertical asymptotes) and the linear right‐side. Therefore, for any real parameters (with the necessary non–degeneracy conditions) the quartic has exactly two real roots and the other two must be non–real complex conjugates.

Thus, the equation necessarily has two real and two imaginary roots.

Summary Explanation (minimal):

  1. Multiply both sides by (x−α)(x−β)(x−γ)(x-\alpha)(x-\beta)(x-\gamma) to obtain a quartic.

  2. With a2,b2,c2>0a^2,b^2,c^2>0 and distinct real α,β,γ\alpha,\beta,\gamma, the hyperbolic terms force sign changes in the intervals (α,β)(\alpha,\beta) and (β,γ)(\beta,\gamma) giving exactly two real roots.

  3. Since the quartic has 4 roots and coefficients are real, the other two are complex conjugates.