Question
Question: Equal volume of two immiscible liquids of densities \(\rho \) and \(2\rho \) are filled in a vessel ...
Equal volume of two immiscible liquids of densities ρ and 2ρ are filled in a vessel as shown in the figure. Two small holes are made at depth 2h and 23h from the surface of the lighter liquid. If v1 and v2 are the velocities of efflux at these two holes, then v2v1 will be
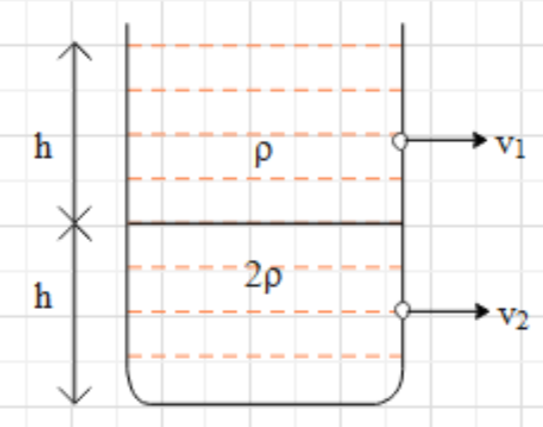
A. 21
B. 221
C. 21
D. 21
Solution
Use Bernoulli’s theorem to find the two velocities of efflux. The Bernoulli’s theorem for two points A and B is given as ρAghA+21ρAvA2=ρBghB+21ρBvB2, where the pressures at A and B are ρA and ρB, depths of A and B are hA and hB. vA and vB are the velocities of the liquid at the points A and B respectively.
Formula used:
ρAghA+21ρAvA2=ρBghB+21ρBvB2
Complete step-by-step solution:
In the given case, there is a container in which two immiscible liquids are present. Since the two liquids are immiscible, they will not interact and mix with each other. Hence, the liquid, which has the least density will be at the top and the liquid with higher density will set down. It is given that the heights of both the liquid layers are equal to h.
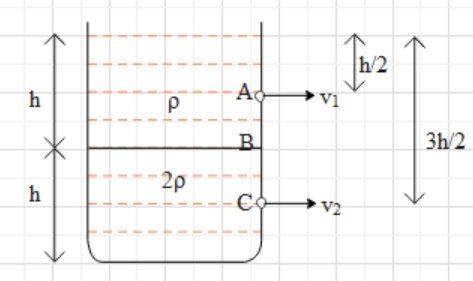
Now, we punch two holes in the container. One hole at a depth of 2h and the other at 23h, both from the surface of the top liquid (as shown). Due to these holes, the liquids come with velocities v1 and v2.
Therefore, there is a flow of both the liquids. When there is a flow of liquid, Bernoulli's theorem comes into role.
Let us apply Bernoulli's theorem, at the points A and B.
Hence, we get,
ρg(2h)+21ρv12=ρgh+0
⇒21v12=g(2h)
⇒v12=gh
⇒v1=gh.
Therefore, the speed of the liquid coming out from point A is v1=gh.
Now, apply the Bernoulli’s theorem at points B and C.
ρgh+0=(2ρ)g(23h)+21(2ρ)v22
⇒gh=2g(23h)+v22
⇒v22=2gh
⇒v2=2gh.
Therefore, the speed of the liquid coming out from point C is v2=2gh.
Therefore, v2v1=2ghgh=21
Hence, the correct option is A.
Note: When a liquid comes out of holes made in the container, the velocity of the liquid is called the velocity of efflux and is given as v=2gH,
Where H is the depth of the hole from the top surface where the liquid is in contact with air.
Therefore, v1=2g(2h)=gh.
Then we can find v2 by applying Bernoulli’s theorem at points A and C.
