Question

Equal charges $Q$ are placed at the four corners A, B, C and D of square of length $a$ . The magnitude of the force on the charge at B will be:
(A) $\dfrac{{3{Q^2}}}{{4\pi {\varepsilon _0}{a^2}}}$
(B) $\dfrac{{4{Q^2}}}{{4\pi {\varepsilon _0}{a^2}}}$
(C) $\dfrac{{k{Q^2}}}{{{a^2}}}\left( {\dfrac{{2\sqrt 2 + 1}}{2}} \right)$
(D) $\left( {2 + \dfrac{1}{{\sqrt 2 }}} \right)\dfrac{{3{Q^2}}}{{4\pi {\varepsilon _0}{a^2}}}$

Answer 1

Hint : As there is no specification in question the charge is positive or negative that is why we have to consider the charge as positive. Calculate the net force acting on the required point here. B. angles of square are always right angled.

Complete Step By Step Answer:
Based on the conditions given in the figure let us draw a suitable diagram as follows:

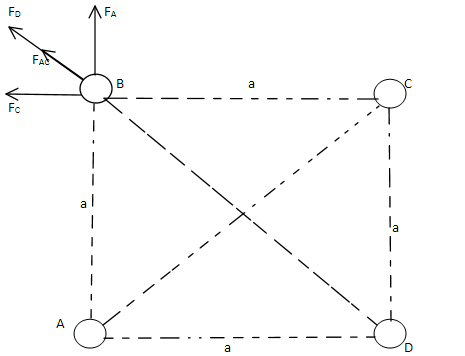
$Q$ is the charge on the corners of the square and $a$ is the length of the side of the square.
Force is given by:
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$ …….(general formula of electrostatic force) $(1)$
$\Rightarrow$ $F = \dfrac{{k{Q^2}}}{{{a^2}}}$…….(charge and side of square is given) $(2)$
From $eq(1)$ and $(2)$ ,
$\Rightarrow {F_A} = \dfrac{{k{Q^2}}}{{{a^2}}}$ ; ${F_C} = \dfrac{{k{Q^2}}}{{{a^2}}}$ and ${F_D} = \dfrac{{k{Q^2}}}{{2{a^2}}}$ …… $(3)$
Net force between the forces ${F_A}$ and ${F_C}$ is given by
$\Rightarrow {F_{net}} = \sqrt {F_A^2 + F_C^2 + 2{F_A}{F_C}\cos \theta }$……..( ${F_A}$ and ${F_C}$ are perpendicular to each other ) $(4)$
$\Rightarrow {F_{net}} = \sqrt 2 {F_A}$………(from $(3)$ )
$\Rightarrow {F_{net}} = \sqrt 2 \dfrac{{k{Q^2}}}{{{a^2}}}$ ……… (from $(3)$ )
Now, overall net force on corner B is given by
$F_{net}' = {F_{net}} + {F_D}$
$= \sqrt 2 \dfrac{{k{Q^2}}}{{{a^2}}} + \dfrac{{k{Q^2}}}{{2{a^2}}}$
$= \dfrac{{k{Q^2}}}{{{a^2}}}\left( {\sqrt 2 + \dfrac{1}{2}} \right)$
$= \dfrac{{k{Q^2}}}{{{a^2}}}\left( {\dfrac{{2\sqrt 2 + 1}}{2}} \right)$
Therefore, the net force can be called as magnitude of force on B is $\dfrac{{k{Q^2}}}{{{a^2}}}\left( {\dfrac{{2\sqrt 2 + 1}}{2}} \right)$
Correct answer is option C.

Note :
In the above question we have calculated the magnitude of forces between the force ${F_A}$ and ${F_C}$ , the angle between them is ${90^0}$ . Therefore, $\cos \theta = 0$ thus the term becomes $zero$ in equation $(4)$ .
Finally the magnitude of force on B is the magnitude of forces ${F_{net}}$ and ${F_D}$ .