Question

Equal charges each of $20\mu C$ are placed at x=0, 2, 4, 8, 16 cm on X-axis. Find the force experienced by the charge at x=2cm.

Answer 1

Apply coulomb’s law. Coulomb’s law states that force between any two point charges is directly proportional to the product of two charges and inversely proportional to the square of distance between them. Also apply the principle of superposition to find the resultant force.

Formula used:
According to Coulomb’s law,
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{qQ}{{{r}^{2}}}$
Q and q are magnitude of charges
r is the distance between the two point charges.
Where,
$k=\dfrac{1}{4\pi {{\varepsilon }_{0}}}$
Where ${{\varepsilon }_{0}}$is the permittivity of free space

Complete answer:
Let ${{q}_{1}},{{q}_{3}},{{q}_{4}},{{q}_{5}}$ be the charges at x=0 ,2, 4,8, 16 cm on X-axis.
The magnitude of charge q is,
${{q}_{1}}={{q}_{2}}={{q}_{3}}={{q}_{4}}={{q}_{5}}=q$
Hence $q=20\mu C$

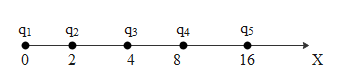
Considering the resultant force as F. F will be the sum of forces ${{F}_{1}},{{F}_{3}},{{F}_{4}},{{F}_{5}}$.
${{F}_{1}}$ is the force on ${{q}_{2}}$due to ${{q}_{1}}$, ${{F}_{3}}$ is the force on ${{q}_{2}}$due to ${{q}_{3}}$, ${{F}_{4}}$ is the force on ${{q}_{2}}$due to${{q}_{4}}$and ${{F}_{5}}$ is the force on ${{q}_{2}}$due to ${{q}_{5}}$.
Thus the resultant force is,
$F={{F}_{1}}+{{F}_{3}}+{{F}_{4}}+{{F}_{5}}$
$F=\dfrac{k{{q}_{2}}{{q}_{1}}}{{{\left( {{r}_{21}} \right)}^{2}}}+\dfrac{k{{q}_{2}}{{q}_{3}}}{{{\left( {{r}_{23}} \right)}^{2}}}+\dfrac{k{{q}_{2}}{{q}_{4}}}{{{\left( {{r}_{24}} \right)}^{2}}}+\dfrac{k{{q}_{2}}{{q}_{5}}}{{{\left( {{r}_{25}} \right)}^{2}}}$
Since,
${{q}_{1}}={{q}_{2}}={{q}_{3}}={{q}_{4}}={{q}_{5}}=q$
$q=20\mu C$
Thus the equation becomes,
$F=\dfrac{k{{q}^{2}}}{{{\left( {{r}_{21}} \right)}^{2}}}+\dfrac{k{{q}^{2}}}{{{\left( {{r}_{23}} \right)}^{2}}}+\dfrac{k{{q}^{2}}}{{{\left( {{r}_{24}} \right)}^{2}}}+\dfrac{k{{q}^{2}}}{{{\left( {{r}_{25}} \right)}^{2}}}$
Since $k{{q}^{2}}$is common in all terms we can take this outside as,
$F=k{{q}^{2}}\left[ \dfrac{1}{{{\left( {{r}_{21}} \right)}^{2}}}+\dfrac{1}{{{\left( {{r}_{23}} \right)}^{2}}}+\dfrac{1}{{{\left( {{r}_{24}} \right)}^{2}}}+\dfrac{1}{{{\left( {{r}_{25}} \right)}^{2}}} \right]$
Then substituting the values in the above equation we get, $F=9\times {{10}^{9}}\times {{\left( 20\times {{10}^{-6}} \right)}^{2}}\left[ \dfrac{1}{{{\left( 2\times {{10}^{-2}} \right)}^{2}}}+\dfrac{1}{{{\left( 2\times {{10}^{-2}} \right)}^{2}}}+\dfrac{1}{{{\left( 6\times {{10}^{-2}} \right)}^{2}}}+\dfrac{1}{{{\left( 14\times {{10}^{-2}} \right)}^{2}}} \right]$
$F=3.6\left[ 0.25+0.25+0.0277+0.0051 \right]\times {{10}^{4}}$
$F=3.6\times \left[ 0.5328 \right]\times {{10}^{4}}$
$F=1.88568\times {{10}^{4}}$
$F=1.89\times {{10}^{4}}N$
Thus the answer is $1.89\times {{10}^{4}}N$.

Note:
Coulomb's law can be described as an inverse square law. Because the force between any two point charges is inversely proportional to the square of distance between them. Gravitational force is also an example of force which satisfies inverse square law. Force exerted per unit charge is known as electric field.