Question

Energy stored in $5\mu F$ and $8\mu F$ capacitors are:
(A). $250\times {{10}^{-6}}\,J,\,36\times {{10}^{-4}}\,J$
(B). $250\times {{10}^{-6}}\,J,\,240\times {{10}^{-4}}\,J$
(C). $250\times {{10}^{-6}}\,J,\,40\times {{10}^{-4}}\,J$

Answer 1

In a circuit, capacitors are connected in different combinations; series and parallel. In series combination, the capacitors are connected one after the other while in parallel combination; the capacitors are connected between two points. The energy stored on each capacitor depends on its capacitance and its potential drop.

Formulae used:
$C=\dfrac{Q}{V}$
$C={{C}_{1}}+{{C}_{2}}+{{C}_{3}}$
$\dfrac{1}{C'}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+\dfrac{1}{{{C}_{3}}}$

Complete step-by-step solution:
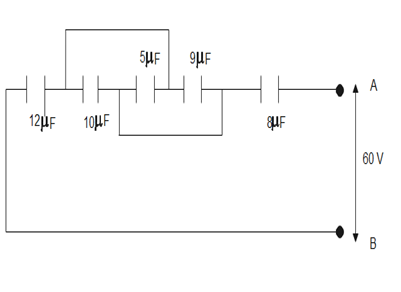
Given different capacitors are in combinations and a potential difference of $60V$ is applied across the end of the circuit.
The capacitance is given by-
$C=\dfrac{Q}{V}$
Here,
$C$ is the capacitance
$Q$ is the charge on capacitor
$V$ is the voltage

The combinations possible in capacitors are series and parallel.
Therefore, labeling the different points in the circuit as-

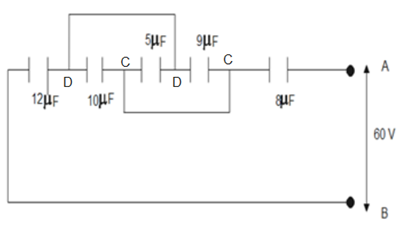
The different capacitors connected in the circuit between point, the circuit can be simplified as-

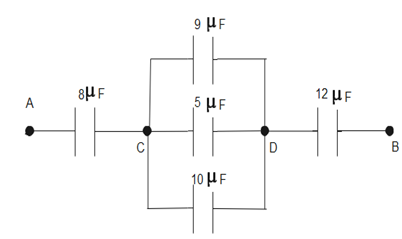
We can see that all the capacitors are in series, therefore, the equivalent capacitance is-

The equivalent of capacitors between points C and D is-
$\begin{aligned} & C={{C}_{1}}+{{C}_{2}}+{{C}_{3}} \\\ & \Rightarrow C=9+5+10 \\\ & \therefore C=24\mu F \\\ \end{aligned}$

The equivalent of all capacitors between points A and B is-
$\begin{aligned} & \dfrac{1}{C'}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+\dfrac{1}{{{C}_{3}}} \\\ & \Rightarrow \dfrac{1}{C'}=\dfrac{1}{8}+\dfrac{1}{24}+\dfrac{1}{12} \\\ & \Rightarrow \dfrac{1}{C'}=\dfrac{3+1+2}{24} \\\ & \therefore C'=4\mu F \\\ \end{aligned}$

We know that,
$C=\dfrac{Q}{V}$

Since the capacitors are connected in series, the charge on all is same, therefore,
$C\propto \dfrac{1}{V}$ - (1)

Therefore, the potential drop on capacitor of$8\mu F$will be-
$\begin{aligned} & \dfrac{8}{4}=\dfrac{60}{{{V}_{1}}} \\\ & \Rightarrow {{V}_{1}}=\dfrac{60\times 4}{8} \\\ & \therefore {{V}_{1}}=30V \\\ \end{aligned}$

The potential drop on $8\mu F$ capacitor is $30V$. We can calculate the energy stored on a capacitor as-
$E=\dfrac{1}{2}C{{V}^{2}}$ - (2)

In the above equation, we substitute values to get,
$\begin{aligned} & E=\dfrac{1}{2}\times 8\times {{10}^{-6}}\times {{(30)}^{2}} \\\ & \therefore E=36\times {{10}^{-4}}J \\\ \end{aligned}$

The energy stored on $8\mu F$ capacitor is $36\times {{10}^{-4}}J$.

From equation (1), the potential on $24\mu F$ capacitor is-
$\begin{aligned} & \dfrac{24}{4}=\dfrac{60}{{{V}_{2}}} \\\ & \Rightarrow {{V}_{2}}=\dfrac{60\times 4}{24} \\\ & \therefore {{V}_{2}}=10V \\\ \end{aligned}$

The potential on $24\mu F$ capacitor is $10V$. Since the potential on capacitors connected in parallel is equal, so the potential on $9\mu F,\,\,5\mu F,\,10\mu F$ is $10V$.
The potential of $5\mu F$ capacitor is $10V$.

From eq (2), the energy stored on the $5\mu F$ capacitor is-
$\begin{aligned} & E'=\dfrac{1}{2}\times 5\times {{10}^{-6}}\times {{(10)}^{2}} \\\ & \therefore E'=250\times {{10}^{-6}}J \\\ \end{aligned}$

The energy stored on $5\mu F$ is $250\times {{10}^{-6}}J$.

Therefore, the energy stored on $8\mu F$ capacitor is $36\times {{10}^{-4}}J$ and the energy stored on $5\mu F$ is $250\times {{10}^{-6}}J$.

Hence, the correct option is (A).

Note:
The combination of capacitors is analogous to the combination of resistors. When a wire is used to join two points, the potential of both points is equal. In series, the charge stored on the capacitors is equal while in parallel, the potential drop on capacitors is equal.