Question

Energy per unit volume for a capacitor having area A and separation d kept at potential difference V is given by:
$\begin{aligned} & A.\quad \dfrac{1}{2}{{\in }_{0}}\dfrac{{{V}^{2}}}{{{d}^{2}}} \\\ & B.\quad \dfrac{1}{2{{\in }_{0}}}\dfrac{{{V}^{2}}}{{{d}^{2}}} \\\ & C.\quad \dfrac{1}{2}{{C}^{\dfrac{1}{2}}} \\\ & D.\quad \dfrac{{{\in }_{0}}^{2}}{2C} \\\ \end{aligned}$

Answer 1

Making a diagram of a parallel plate capacitor will be helpful. We will then find the capacitance (C) given by; $C=\dfrac{{{\in }_{0}}A}{d}$. The energy of a parallel plate capacitor (E) is given by; $E=\dfrac{1}{2}C{{V}^{2}}$. Finally, to find the energy per unit volume, we will divide the value of the energy by the volume of the parallel plate capacitor.

Step by step solution:
Let’s make a diagram of a parallel plate capacitor having plate area (A) and the distance between the plates be (d). The distance between the plates be (d). Since, the potential difference between the plates of the capacitor is V, hence, we will consider one of the plates to be at potential (V) and another plate to have potential zero.

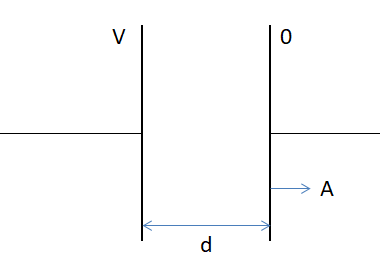
Hence, the capacitance of the parallel plate capacitor (C) is: $C=\dfrac{{{\in }_{0}}A}{d}$.
The electrical energy stored in the parallel plate capacitor is given by; $E=\dfrac{1}{2}C{{V}^{2}}$.
Substituting in the value of the capacitance from above into the value of the energy of the capacitor, we get; $E=\dfrac{1}{2}C{{V}^{2}}\Rightarrow E=\dfrac{1}{2}\left( \dfrac{{{\in }_{0}}A}{d} \right){{V}^{2}}$.
The volume of the parallel plate capacitor is given by the product of the Area (A) times the distance of separation between the plates of the capacitor (d), Hence the value of the volume is: $Vol=Ad$.
The energy density of the capacitor (U) is given by dividing the value of the energy of the capacitor by the volume, that is; $U=\dfrac{E}{Vol}\Rightarrow U=\dfrac{\dfrac{1}{2}\left( \dfrac{{{\in }_{0}}A}{d} \right){{V}^{2}}}{Ad}\Rightarrow U=\dfrac{1}{2}\left( \dfrac{{{\in }_{0}}}{{{d}^{2}}} \right){{V}^{2}}$.
Hence, the Energy per unit volume of the capacitor is given by: $U=\dfrac{1}{2}\left( \dfrac{{{\in }_{0}}}{{{d}^{2}}} \right){{V}^{2}}$.

Note: It’s important to remember that there are multiple formulas to find the electrical energy, however the energy depends upon the kind of the electrical component used. Such as for the case of a parallel plate capacitor, the electrical energy is given by: $E=\dfrac{1}{2}C{{V}^{2}}$ and for an inductor, the energy will be: $E=\dfrac{1}{2}L{{I}^{2}}$. Similarly for a resistor, the energy will be: $E={{I}^{2}}R$.