Question

Empty space in ccp lattice is
(A) 26%
(B) 45%
(C) 90%
(D) 30%

Answer 1

To calculate the empty space in ccp lattice, you should know its packing efficiency value. Packing efficiency is the percentage of total space filled by the particles/atoms out of the total space available. After calculating the packing efficiency of ccp lattice, subtract it from 100% and then you will get the empty space in ccp lattice.

Complete step by step solution:
Packing efficiency in ccp (cubic close packing) lattice:

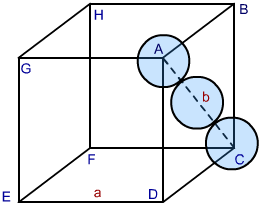
Cubic close packing is an efficient type of packing. Let us calculate the efficiency of packing in ccp structure. The above figure is a unit cell of ccp structure. In the figure let the unit cell edge length be ‘a’ and face diagonal AC= b.
Now, in $\Delta {\text{ ABC}}$ ,
${\text{A}}{{\text{C}}^{\text{2}}}{\text{ = B}}{{\text{C}}^{\text{2}}}{\text{ + A}}{{\text{B}}^{\text{2}}}{\text{(by pythagoras theorem)}}$
${b^2} = {a^2} + {a^2} = 2{a^2}$
Or, $b = \sqrt 2 a$
Let r is the radius of the sphere, therefore,
$b = 4r = \sqrt 2 a$
Or, $a = 4r/\sqrt 2 = 2\sqrt 2 r$
We can also write, $r = \dfrac{a}{{2\sqrt 2 r}}$ .
We also know that each unit cell in the ccp structure has effectively 4 spheres or atoms. Therefore, the total volume of four spheres is equal to $4 \times (4/3)\pi {r^3}$ and the volume of the cube is ${a^3}$ or ${(2\sqrt 2 r)^3}$.
Packing efficiency = $\dfrac{{{\text{volume occupied by four spheres in the unitcell }} \times 100}}{{{\text{total volume of the unit cell}}}}\%$
Packing efficiency = $\dfrac{{4 \times (4/3)\pi {r^3} \times 100}}{{{{(2\sqrt 2 r)}^3}}}\% = 74\%$ Thus, the total space occupied by the atoms in the ccp structure is 74%. Hence, the empty space will be 26% ($100\% - 74\% = 26\%$ ).

Therefore, option A is the correct answer.

Note: Both face-centred cubic (fcc) lattice or cubic close packing (ccp) are the same. Here, atoms, besides being located at the corners, are also present at the centre of the six faces. Each of these atoms is shared between two adjacent unit cells and only half of each atom belongs to a unit cell. Thus, their contribution to the unit cell is:
8 corner atoms $\times$ 1/8 atom per unit cell = 1 atom
6 face-centred atoms $\times$ 1/2 atom per unit cell = 3 atoms.
$\therefore$ Total number of atoms per unit cell in fcc or ccp = 4 atoms.