Question
Question: Find the locus of the middle points of chords of an ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ whic...
Find the locus of the middle points of chords of an ellipse a2x2+b2y2=1 which are drawn through the positive end of the minor axis.
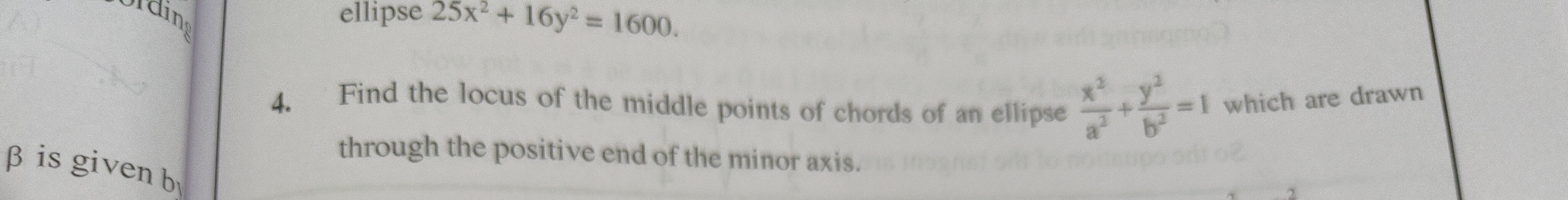
a2x2+b2y2−by=0
a2x2+b2y2+by=0
a2x2−b2y2−by=0
a2x2−b2y2+by=0
a2x2+b2y2−by=0
Solution
Let the ellipse be a2x2+b2y2=1. Assume a>b, so the positive end of the minor axis is (0,b). Let M(h,k) be the midpoint of a chord passing through (0,b). Let the endpoints of the chord be P(x1,y1) and Q(x2,y2). The midpoint M(h,k) has coordinates h=2x1+x2 and k=2y1+y2. The equation of the chord with midpoint (h,k) is given by T=S1, where T=a2xh+b2yk and S1=a2h2+b2k2. So, the equation of the chord is a2xh+b2yk=a2h2+b2k2. Since this chord passes through the point (0,b), we substitute x=0 and y=b into the equation of the chord: a2(0)h+b2(b)k=a2h2+b2k2 bk=a2h2+b2k2 Rearranging the terms to find the locus of (h,k): a2h2+b2k2−bk=0 Replacing h with x and k with y to get the locus equation: a2x2+b2y2−by=0
This equation represents an ellipse. It can be rewritten as: a2x2+b21(y2−by)=0 a2x2+b21(y2−by+4b2−4b2)=0 a2x2+b21((y−2b)2−4b2)=0 a2x2+b2(y−2b)2−41=0 a2x2+b2(y−2b)2=41 a2/4x2+b2/4(y−b/2)2=1 This is the equation of an ellipse with center (0,b/2) and semi-axes a/2 and b/2.
