Question
Question: $\ell = 30m$ $\underline{m}$ ? ...
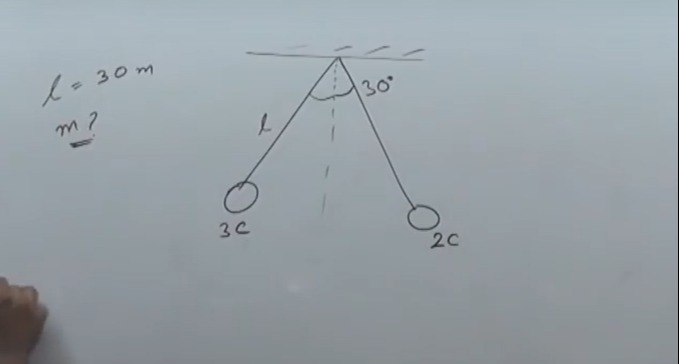
ℓ=30m
m ?
Answer
m≈8.55×107kg.
Explanation
Solution
We have two identical spheres (mass = m) hanging by strings of length ℓ = 30 m. They carry charges 3 C (left) and 2 C (right) and are in electrostatic equilibrium. The strings make an angle of 15° with the vertical (since the total angle between them is 30°).
For each sphere, resolve the forces:
- Weight: mg downward.
- Tension: T along the string.
- Electrostatic repulsion: Fe horizontally.
In equilibrium,
Tcos15∘=mgandTsin15∘=Fe.Dividing,
tan15∘=mgFe⟹m=gtan15∘Fe.The horizontal repulsive force between the spheres is given by Coulomb’s law:
Fe=kd2(3)(2)=d26k,where k=9×109Nm2/C2 and the separation d is determined by the horizontal displacement of each sphere:
d=2ℓsin15∘.Thus,
d2=4ℓ2sin215∘.So,
Fe=4ℓ2sin215∘6k=2ℓ2sin215∘3k.Substitute Fe into the m-equation:
m=2ℓ2sin215∘gtan15∘3k.Inserting numerical values:
- ℓ = 30 m,
- k=9×109Nm2/C2,
- g=9.8m/s2,
- sin15∘≈0.258819 so that sin215∘≈(0.258819)2≈0.066987,
- tan15∘≈0.267949.
Now,
m=2×(30)2×0.066987×9.8×0.2679493×9×109.Calculate step‐by‐step:
- (30)2=900.
- Denominator factor: 2×900=1800.
- Then, 1800×0.066987≈120.376.
- Next, 120.376×9.8≈1179.725.
- And then, 1179.725×0.267949≈315.75.
The numerator is:
3×9×109=27×109.Thus,
m≈315.7527×109≈85.5×106kg=8.55×107kg.