Question

A charge q is placed at the centre of the cubical vessel (with one face open) as shown in figure. The flux of the electric field through the surface of the vessel is -

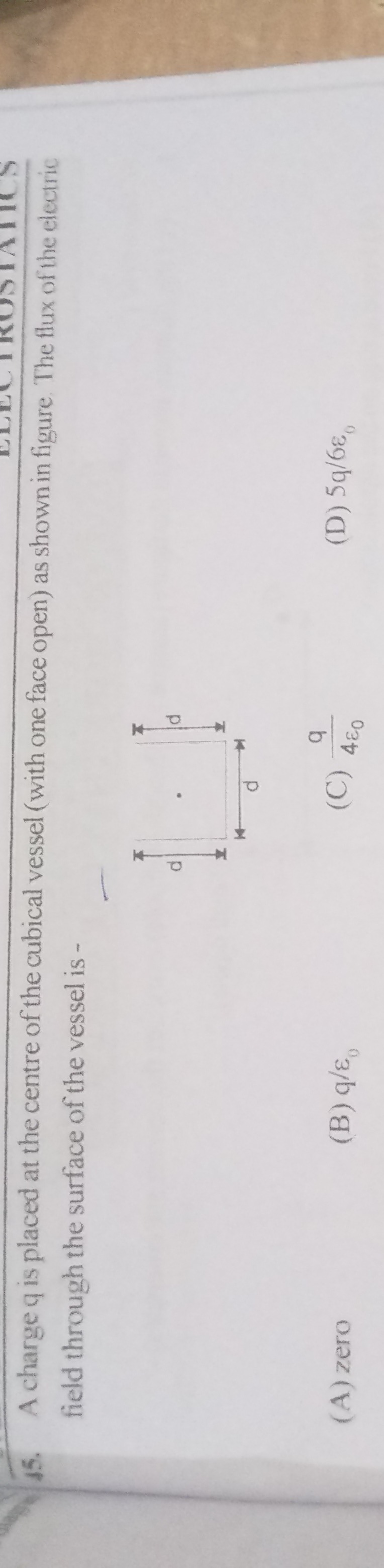
• A. zero
• B. $\frac{q}{\epsilon_0}$
• C. $\frac{q}{4\epsilon_0}$
• D. $\frac{5q}{6\epsilon_0}$

Answer 1

Answer: (D)

$\frac{5q}{6\epsilon_0}$

Answer 2

The problem asks for the electric flux through the surface of a cubical vessel with one face open, with a charge $q$ placed at its center.

We can solve this problem using Gauss's Law. Gauss's Law states that the total electric flux through a closed surface is equal to the enclosed charge divided by the permittivity of free space, i.e., $\Phi = \oint_S \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{enclosed}}{\epsilon_0}$.

The given surface is an open cubical vessel, which is not a closed surface. To apply Gauss's Law, we can consider a complete closed cube by imagining the open face is closed. The charge $q$ is at the center of this complete closed cube.

According to Gauss's Law, the total electric flux through the entire closed cube is $\Phi_{total} = \frac{q}{\epsilon_0}$, since the charge $q$ is enclosed within the closed surface.

A complete cube has 6 faces. Since the charge is placed at the center of the cube, the electric field lines emanate radially from the charge and pass through all 6 faces. Due to the symmetry of the cube and the central position of the charge, the electric flux through each of the 6 faces is equal.

Let $\Phi_{face}$ be the electric flux through one face of the closed cube. Since there are 6 faces, the total flux is the sum of the flux through each face: $\Phi_{total} = 6 \Phi_{face}$. Therefore, the flux through one face of the closed cube is: $\Phi_{face} = \frac{\Phi_{total}}{6} = \frac{q}{6\epsilon_0}$.

The cubical vessel has one face open. This means the vessel consists of 5 faces of the complete cube. The flux through the surface of the vessel is the sum of the fluxes through these 5 faces. Let $\Phi_{vessel}$ be the flux through the surface of the vessel. Since the flux through each face of the complete cube is $\frac{q}{6\epsilon_0}$, the flux through the 5 faces of the vessel is: $\Phi_{vessel} = 5 \times \Phi_{face} = 5 \times \frac{q}{6\epsilon_0} = \frac{5q}{6\epsilon_0}$.

Alternatively, let the open face be the top face. The total flux through the closed cube is the sum of the flux through the vessel (bottom face and four side faces) and the flux through the open top face. $\Phi_{total} = \Phi_{vessel} + \Phi_{open face}$. We know $\Phi_{total} = \frac{q}{\epsilon_0}$ and $\Phi_{open face} = \frac{q}{6\epsilon_0}$ (since it is one face of the symmetric cube). So, $\frac{q}{\epsilon_0} = \Phi_{vessel} + \frac{q}{6\epsilon_0}$. $\Phi_{vessel} = \frac{q}{\epsilon_0} - \frac{q}{6\epsilon_0} = \frac{6q - q}{6\epsilon_0} = \frac{5q}{6\epsilon_0}$.