Question
Question: Electrostatic potential at H is A. \[\dfrac{\sigma }{{^{{\varepsilon _0}}}}\left[ {{{\left( {{a^2...
Electrostatic potential at H is
A. ε0σ[(a2−H2)1/2−H]
B. ε0σ[(a2−H2)1/2+H]
C. 2ε0σ[(a2+H2)1/2−H]
D. 2ε0σ[(a2−H2)1/2−H]
Solution
In this question,we are going to use the concept of electrostatic potential and derive the expression of it by assuming certain assumptions.The
potential due to point charge is inversely proportional to square root of distance.
Complete step by step answer:
First let’s calculate potential due to a ring on a point lying on its axis, then we will use it to calculate potential due to disc.
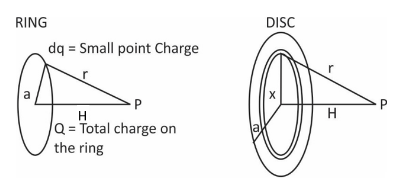
Consider a small point charge on the ring having small charge dq. Now potential due to this point charge can be written as
dv=r2K(dq)
Total potential due to ring: V=∫dv
V=∫r2K(dq)
r=H2+a2
V=∫H2+a2K(dq)
V=H2+a2K∫dq
V=H2+a2KQ
Now, Consider a small ring in a thin disc, the small ring has radius =xand thickness=dx. As we have already calculated the potential due to ring, we can say that potential due to the small ring is
dV=H2+x2Kdq
Now, we can integrate thin disc to get potential of entire disc
V=∫dV
V=∫H2+x2Kdq
Now we have to substitute dq charge in small ring to thickness dx in terms of x,
dq=TotalareaTotalcharge×Areaofsmallring
dq=πa2Q×(2πx)×dx
Area of ring is calculated by approximating small ring as rectangle of length equal to circumference of small ring and height equal to the thickness
V=∫(πa2)(H2+x2)KQ2πxdx
V=a2KQ∫H2+x22xdx
Here the limit of x is from 0 to a
So, V=a2KQ∫0aH2+x22xdx ….. (i)
Now, SubstitutingH2+x2=t, putting for lower limit x=0then H2+02=t ⇒t=H2 now for upper limit x=a then H2+a2=t,
H2+x2=t
Differentiating, t with respect to x so, 2x dx=dt
Putting all above values in equation (i).
V=a2KQ∫H2H2+a2tdt
V=a2KQ2(H2+a2−H2) V=a2KQ2(H2+a2−H)
Putting K=4πε01 and σ=πa2Q, we get
V=2εoσ(H2+a2−H)
Here option (C) is the correct option.
Note: As the limits of xis from 0to aand H2+x2=t
at x=0, t=H2
at x=a, t=H2+a2
So, the limits of twill be from H2to H2+a2
