Question

Electric potential V due to a spherically symmetrical charge system varies with distance r as shown in the figure. Given for and for which of the following statements are true?

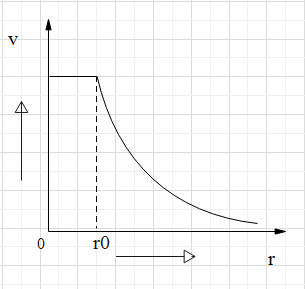
A. Electric field due to the charge system is discontinuous at $r={{r}_{0}}$
B. The net charge enclosed in a sphere of radius $r=2{{r}_{0}}$ is Q
C. No charge exists at any point in a spherical region on radius $r<{{r}_{0}}$
D. Electrostatic energy inside the sphere of radius $r={{r}_{0}}$ is zero

Answer 1

This question is based on the properties of the electric field, the charge and the electrostatic energy of the charged sphere. Using the properties like the electric field inside the sphere is zero, the charges are uniformly distributed all over the surface of a charged sphere, the solution can be obtained.

Formula used:
$E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}}$
$U=\int{{{E}^{2}}d\tau }$

Complete step-by-step answer:
Let us consider the statements of the options given. So, we have,
A. Electric field due to the charge system is discontinuous at $r={{r}_{0}}$
From point 0 to ${{r}_{0}}$ , the charge is constant, that is, it is zero. After the point ${{r}_{0}}$ , the charge is being represented as flowing from the infinity. For the distance up to $r<{{r}_{0}}$ , the electric field is zero, thus, the charge enclosed is zero. For the distance, $r>{{r}_{0}}$ , the electric field is distributed all over the surface. For the distance $r={{r}_{0}}$ , the electric field changes from zero to some amount. Therefore, this option is true.

B. The net charge enclosed in a sphere of radius $r=2{{r}_{0}}$ is Q
Consider the figure.

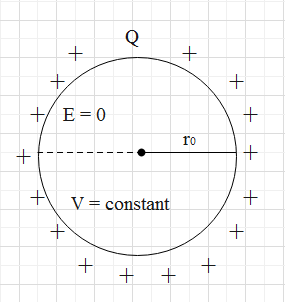
From the figure it’s clear that the radius of the sphere is ${{r}_{0}}$ , so the diameter of the sphere will be $2{{r}_{0}}$ .
As the charges appear on the surfaces of the sphere, thus, the net charge enclosed in the sphere of radius $r=2{{r}_{0}}$ is Q. therefore, this option is true.

C. No charge exists at any point in a spherical region on radius $r<{{r}_{0}}$
The electric field is directly proportional to the charge Q, as given below.

& E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}} \\\ & E\propto Q \\\ \end{aligned}$$ Where Q is the charge and r is the radius of the sphere. The electric field inside the sphere is zero, inside the sphere, the distance will be $$r<{{r}_{0}}$$ . As, the electric field is directly proportional to zero, thus the charge enclosed by the sphere will also be zero. Or by Gauss law, the charge enclosed by a closed surface is zero. Therefore, this option is true. D. Electrostatic energy inside the sphere of radius $$r={{r}_{0}}$$ is zero The electrostatic energy formula is given as follows. $$U=\int{{{E}^{2}}d\tau }$$ …… (1) Gauss law, the charge enclosed by a closed surface is zero. The electric field is directly proportional to the charge Q, as given below. $$\begin{aligned} & E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}} \\\ & E\propto Q \\\ \end{aligned}$$ The electric field inside the sphere is zero. Therefore, the equation (1) becomes, $$\begin{aligned} & U=\int{(0)d\tau } \\\ & \Rightarrow U=0 \\\ \end{aligned}$$ **So, the correct answers are “Option A,B,C and D”.** **Note:** The properties of the electric field is the main key point to know. If these are known, then, using the relation between the charge, the potential, the electrostatic field and the electric field, this type of problem can be solved.