Question

Electric potential energy of an Electric dipole in dipole from zero energy position to a particular position (The zero energy position to be one when an electric dipole of dipole moment $p$ is on it such that
$P=p\times E$
This torque will tend to rotate the dipole. Let $dW$ be the small amount of work done. This will turn the dipole through an angle $d\theta$. That is,
$\begin{aligned} & dW={{T}_{ext}}\cdot d\theta \\\ & \Rightarrow dW=pE\sin \theta d\theta \\\ \end{aligned}$
Let $W$ be the work done in turning the dipole from $0{}^\circ$ to $\theta {}^\circ$ then,

& W=\int\limits_{0}^{W}{dW} \\\ & =\int\limits_{90{}^\circ }^{\theta }{pE\sin \theta d\theta } \\\ \end{aligned}$$ Describe these.

Answer 1

potential energy is the energy required by the body in order to take it from the infinity to a specific position according to our need. Torque is the rotational analogue for the force in mechanics. It is the force required for the body in order to rotate in a specific way. This all will help you in answering this question.

Complete answer:
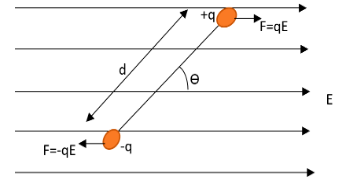
The force experienced by the charges can be shown as $qE$ and $-qE$ , as represented in the diagram.
$\tau =p\times E$
The measure of work done by the external torque can be shown as,
$W=\int\limits_{{{\theta }_{0}}}^{{{\theta }_{1}}}{{{\tau }_{ext}}\left( \theta \right)}d\theta$
Substituting the value of the torque in this will give,
The measure of work done by the external torque can be shown as,
$W=\int\limits_{{{\theta }_{0}}}^{{{\theta }_{1}}}{pE\sin \theta }d\theta =pE\left( \cos {{\theta }_{0}}-\cos {{\theta }_{1}} \right)$
As we all know that the work done in taking a system of charges from infinity to a specific configuration is explained as the potential energy of the system. That is the potential energy of the system can be shown as,
$U\left( \theta \right)=pE\left( \cos {{\theta }_{0}}-\cos {{\theta }_{1}} \right)$

Note:
The electric potential and potential energy are not the same. The major difference is that electric potential at a position in an electric field is the measure of work done to take the unit positive charge from infinity to that position. The electric potential energy is defined as the energy that is required to move a charge against the electric field.