Question

Electric intensity outside a charged cylinder having the charge per unit length $\lambda$ at a distance $r$ from its axis is
A. $E = \;\dfrac{{2\pi {\varepsilon _0}\lambda }}{{k{r^2}}}$
B. $E = \dfrac{{{\varepsilon _0}\lambda }}{{2\pi k{r^2}}}$
C. $E = \dfrac{\lambda }{{2\pi {\varepsilon _0}kr}}$
D. $E = \dfrac{{4\pi {\varepsilon _0}\lambda }}{{k{r^2}}}$

Answer 1

The electric intensity outside the charged cylinder having dimension as per given is calculated by placing a charge outside the cylinder. And by using the Gauss’s theorem, the relation between the charge and the total normal electric intensity is derived.

Useful formula:
Gauss’s theorem states that Total normal electric induction over any closed surface is equal to the total charge enclosed by that surface.
$q = TNEI$
Where, $q$ is the charge enclosed by the surface, $TNEI$ is the Total normal electric induction.

The total normal electric induction over any closed surface is given by,
$TNEI = \int {\varepsilon E\cos \theta ds}$
Where, $\varepsilon$is the permittivity of medium, $E$is the electric field intensity, $\theta$ is the angle between area vector and electric field and $ds$ is the small area enclosed.

Complete step by step answer:
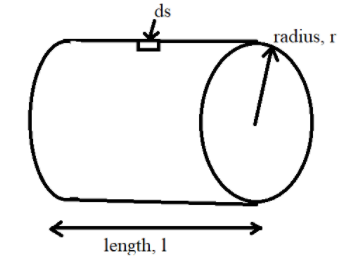
Given, The charge per unit length is $\lambda$,
The radius of the cylinder is $r$.

When a charge $q$ is placed in a free space, it creates some region around itself in which other charge gets attraction or repulsion. This is known as the electric field. Consider an imaginary closed surface area in which the charge $q$ is located then the tubes of induction pass through the area. The total number of tubes of forces passing normally through the whole area is known as total normal electric induction $\left( {TNEI} \right)$.

The total normal electric induction over any closed surface is given by,
$TNEI = \int {\varepsilon E\cos \theta ds\;} ............................\left( 1 \right)$
The charges are uniform in the conduction cylinder. So, there is a symmetry around the imaginary surface. Hence $E$ is constant. The values of permittivity of medium$\varepsilon$ and the angle $\theta$ is Zero. Then,
$TNEI = \varepsilon E\cos 0\int {ds\;}$
Since $cos 0 = 1$ so,
$TNEI = \varepsilon E\int {ds}$
The area of the cylinder is given by $\int {ds = 2\pi rl}$
Where, $r$is the radius of the cylinder, $l$ is the length of the cylinder.
$TNEI = \varepsilon E \times 2\pi rl$

The charge enclosed by the surface is defined by,
$q = \lambda l\;......................................\left( 2 \right)$

By Gauss’s theorem,
$q = TNEI$
Substitute the value of $TNEI$and $q$ values in above equation,
$\lambda l = \varepsilon E \times 2\pi rl \\\ \dfrac{{\lambda l}}{{2\pi rl\varepsilon }} = E \\\ E = \dfrac{\lambda }{{2\pi \varepsilon r}} \\\$
Since, $\varepsilon = {\varepsilon _0}k$
Where, ${\varepsilon _0}$is the permittivity of free space, $\varepsilon$ is the permittivity of medium and $k$ is the proportionality constant.
Substituting the $\varepsilon$value in above equation,
$E = \dfrac{\lambda }{{2\pi {\varepsilon _0}kr}}$

Hence, the option (C) is correct.

Note:
Since, the charge outside the charged cylinder is equal to the total normal electric field intensity of the charged cylinder, using this relation the value of electric field intensity is calculated. The electric field intensity is completely dependent on the charge per unit length of the cylinder, the permittivity of the medium and the radius of the cylinder.