Question

Electric field variation between the plates of capacitor is shown. Find relation between K₁, K₂, K₃, if 2x = y.

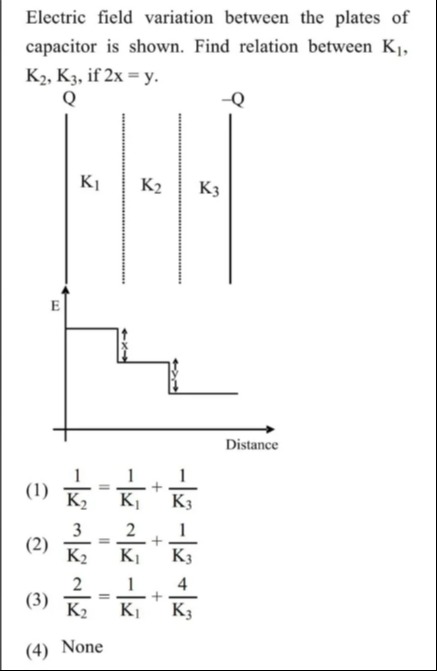
• A. $\displaystyle \frac{1}{K_2} = \frac{1}{K_1} + \frac{1}{K_3}$
• B. $\displaystyle \frac{3}{K_2} = \frac{2}{K_1} + \frac{1}{K_3}$
• C. $\displaystyle \frac{2}{K_2} = \frac{1}{K_1} + \frac{4}{K_3}$
• D. None

Answer 1

Answer: (B)

$\displaystyle \frac{3}{K_2} = \frac{2}{K_1} + \frac{1}{K_3}$

Answer 2

Key idea: Continuous electric displacement $D$ implies

$$D=\varepsilon_0K_1E_1=\varepsilon_0K_2E_2=\varepsilon_0K_3E_3.$$

Thus

$$\frac{E_1}{E_2}=\frac{K_2}{K_1},\quad \frac{E_2}{E_3}=\frac{K_3}{K_2}.$$

The graph shows steps:

$$E_1 - E_2 = x,\quad E_2 - E_3 = y = 2x.$$

Substitute

$$E_1 - E_2 = E_2\Bigl(\frac{K_2}{K_1}-1\Bigr)=x, \quad E_2 - E_3 = E_3\Bigl(\frac{K_2}{K_3}-1\Bigr)=2x.$$

Eliminating $E_2$ and $E_3$ yields after algebra

$$\frac{3}{K_2}=\frac{2}{K_1}+\frac{1}{K_3}.$$