Question
Question: Electric field in a region is given by following equation \(E = \frac{K(\vec{r}-\vec{r_0})}{|\vec{...
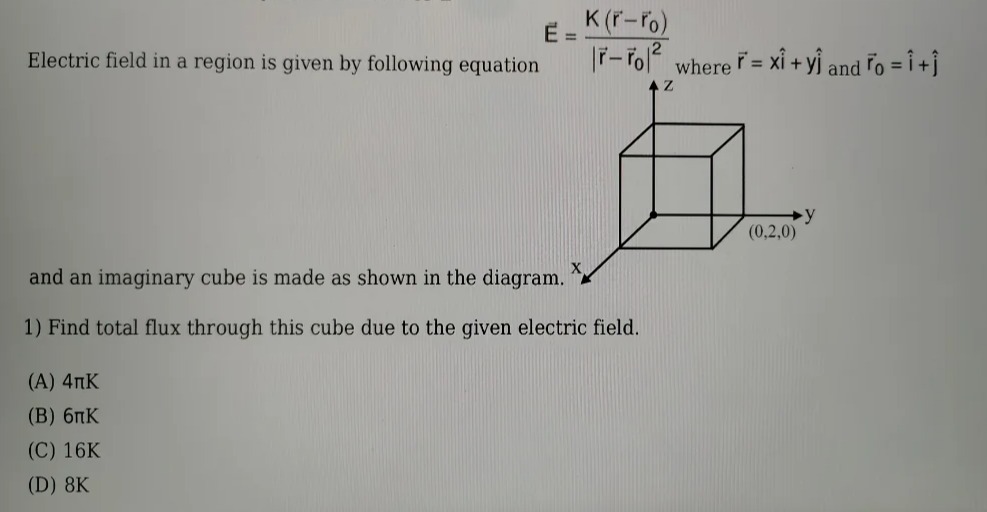
Electric field in a region is given by following equation
E=∣r−r0∣2K(r−r0) where r=xi^+yj^ and r0=i^+j^ and an imaginary cube is made as shown in the diagram.
- Find total flux through this cube due to the given electric field.
A
4πK
B
6πK
C
16K
D
8K
Answer
4πK
Explanation
Solution
Key idea:
- The field can be written in the form
which is the field of a point−singularity located at r0.
- Away from r0, ∇⋅E=0.
- By Gauss’s law, the net flux through a closed surface that encloses the singularity is
- Although r0 lies on the face, one treats it as enclosed for flux count.
Therefore, the total flux through the cube is
4πK.