Question
Question: Electric field in a region is given by \(E=-4x\hat i+6y\hat j\), find the charge enclosed in the cub...
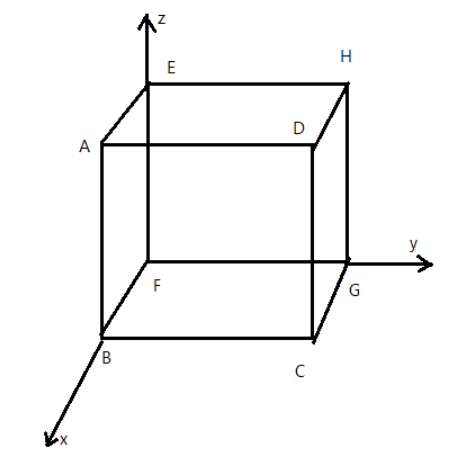
Electric field in a region is given by E=−4xi^+6yj^, find the charge enclosed in the cube side 1m oriented as shown in figure.
Explanation
Solution
Here we have a cube, which is clearly a closed figure. Electric field is the electric force due to a unit positive charge which is at rest would exert on its surrounding. We need to calculate the charge in the cube. But we know that the total charge enclosed in a closed surface is given by Gauss law.
Formula used:
E\cdot dA $$ **Complete answer:** We know that the electric force due to a pair of charges is given by Coulomb's law. An electric field can be produced by a time-varying electric field or an electrical charge. These can be either attracting or repelling in nature. An electric field $E$ is defined as the electric force $F$ per unit positive charge$q$, which is infinitesimally small and at rest, and is given as $E=\dfrac{F}{q}$ From Gauss law, we know that the total electric flux through a closed surface is equal to $\dfrac{1}{\epsilon_{0}}$ times the charge enclosed in the surface, and it is given by $\Phi_{E}=\dfrac{q}{\epsilon_{0}}$ Gauss law can also be given as $${{\Phi }_{_{E}}}=\mathop{{\int\\!\\!\\!\\!\\!\int}\mkern-21mu \bigcirc}\nolimits_E E\cdot dA $$ where $$dA$$ is the surface area vector. This form of Gauss law is called the integral form of Gauss law. Given that $E=-4x\hat i+6y\hat j$ and the charge enclosed in cube side$$1m$$, implies $x=y=z=1$ Then $\Phi=6ydy-4xdx=6\times 1\times 1=4\times 1\times 1=6-4=2$ Then from $\Phi_{E}=\dfrac{q}{\epsilon_{0}}$ we get,$2=\dfrac{q}{\epsilon_{0}}$ Or,$q=2\epsilon_{0}$ **Hence the answer is A.$2\epsilon_{0}$.** **Note:** Electric field is in the direction of the force. Usually, the electric field of a point positive charge is radially outwards, whereas the electric field of a point negative charge is radially inwards to the charge. However, the electric field also depends on the symmetry of the charge carrying conductor.