Question

Electric field due to uniformly charged sphere.

Answer 1

This is the case of solid non-conducting spheres. We will have three cases associated with it . They are : electric fields inside the sphere, on the surface, outside the sphere .
Apply the gauss theorem to find the electric field at the three different places.

Complete step by step solution:
Consider a charged solid sphere of radius $R$ and charge $q$ which is uniformly distributed over the sphere. We will use Gauss Theorem to calculate electric fields. If $\phi$ be the electric flux and $Q$ be the charge then :
${\varepsilon _0}\phi = {Q_{enclosed}}$
Also , electric flux=electric field X area of the enclosed surface : $\phi = EA$
Case I- Inside the sphere $(r < R)$

                     ![](https://www.vedantu.com/question-sets/d78998ec-89b7-435b-8ef0-a5feff33fe787685972523592875793.png)  

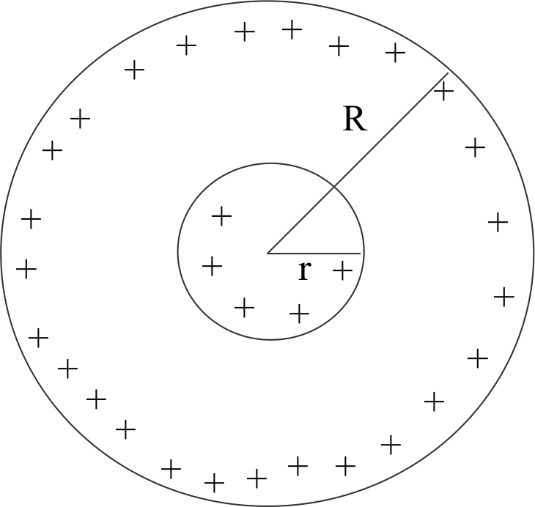
The charge distribution is uniform . Volume density will be the same. Let the charge enclosed by a circle of radius $r$ be $q'$ . Since volume density is same then-
$\dfrac{{q'}}{{\dfrac{4}{3}\pi {r^3}}} = \dfrac{q}{{\dfrac{4}{3}\pi {R^3}}} \\\ q' = q\dfrac{{{r^3}}}{{{R^3}}} \\\$
Applying Gauss Theorem here-
$\phi = E4\pi {r^2} \\\ \dfrac{{{Q_{enclosed}}}}{{{\varepsilon _0}}} = E4\pi {r^2} \\\ \dfrac{{q'}}{{{\varepsilon _0}}} = E4\pi {r^2} \\\ \dfrac{q}{{{\varepsilon _0}}} \times \dfrac{{{r^3}}}{{{R^3}}} = E4\pi {r^2} \\\ E = \dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{{qr}}{{{R^3}}} \\\$
This is the electric field inside the charged sphere .
Case II: On the surface $(r = R)$
In the above case we have calculated the electric field inside the sphere. In that formula we will put $(r = R)$ , so evaluate the electric field on the surface of the sphere .
$E = \dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{{qr}}{{{R^3}}} \\\ E = \dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{{qR}}{{{R^3}}} \\\ E = \dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{q}{{{R^2}}} \\\$
This is the electric field on the surface.
Case III: Outside the sphere $(r > R)$

We will apply Gauss theorem in this too.
$\phi = EA \\\ \dfrac{q}{{{\varepsilon _0}}} = E4\pi {r^2} \\\ E = \dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{q}{{{r^2}}} \\\$
This is the electric field outside the sphere.

If we plot these variations on a graph we will get the following graph:

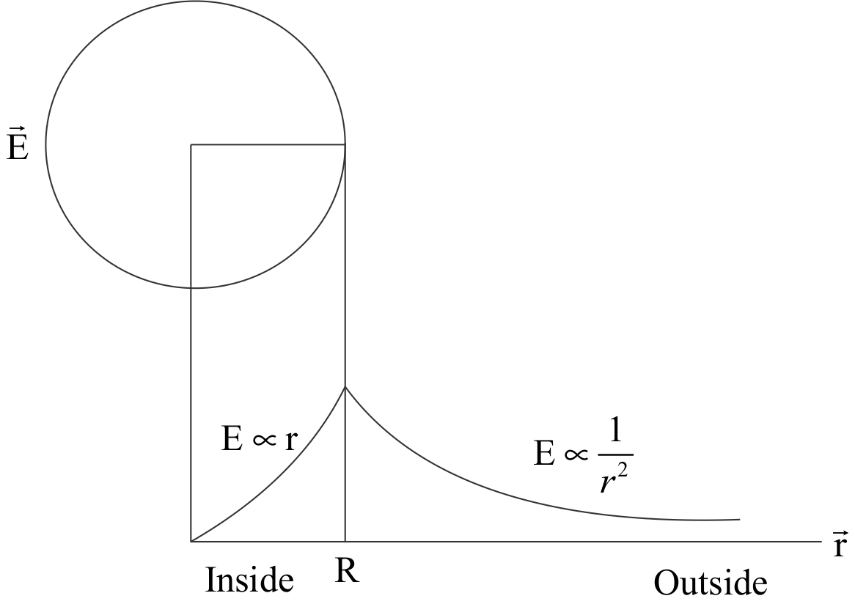
Note: Since this is a solid sphere , it has charge inside it as well and that is why the electric field is non zero. In case of a hollow spherical shell, the electric field inside the shell is zero .