Question
Question: Electric field at point P is given by $\vec{E} = E_0 \hat{r}$. The total flux through the given cyli...
Electric field at point P is given by E=E0r^. The total flux through the given cylinder of radius R height h is:
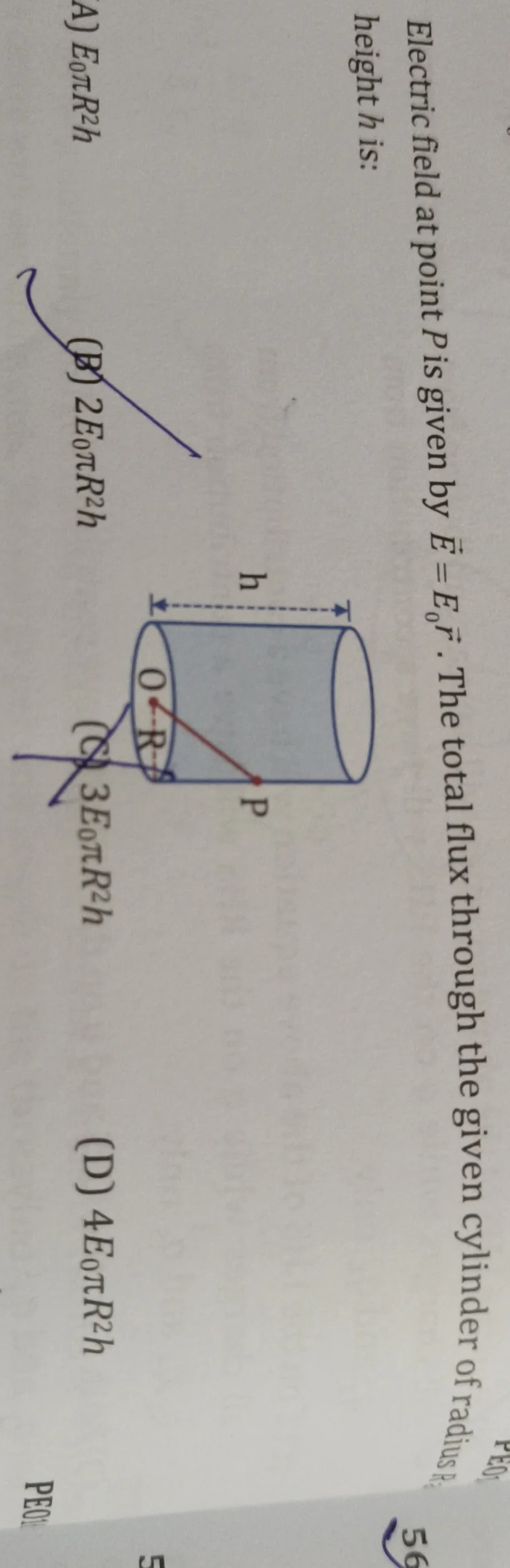
E0πR2h
2E0πR2h
3E0πR2h
4E0πR2h
The provided solution indicates that none of the options match the calculated flux. Therefore, a correct answer cannot be selected from the given options.
Solution
The problem states that the electric field is E=E0r^. If we interpret r^ as a constant radial direction from the center of the cylinder, and E0 as a constant magnitude, the flux through the curved surface of the cylinder is Φside=∫E⋅dA=∫E0dA=E0(2πRh).
However, the provided options are proportional to the volume of the cylinder (πR2h), which suggests a different interpretation or a potential error in the problem statement or options. If the electric field were uniform and directed along the axis of the cylinder, say E=E0k^, the net flux through the closed cylinder would be zero.
Given the discrepancy and the detailed calculation in the provided raw solution leading to a result not matching any option, it's concluded that there might be an issue with the question or its options. The detailed calculation in the raw solution for a radial electric field is complex and does not yield any of the provided answers. Without further clarification or correction, it's impossible to definitively select a correct answer from the given choices.
