Question
Question: The point of maximum and minimum attraction in the curve between potential energy (U) and distance (...
The point of maximum and minimum attraction in the curve between potential energy (U) and distance (r) of a diatomic molecules are respectively.
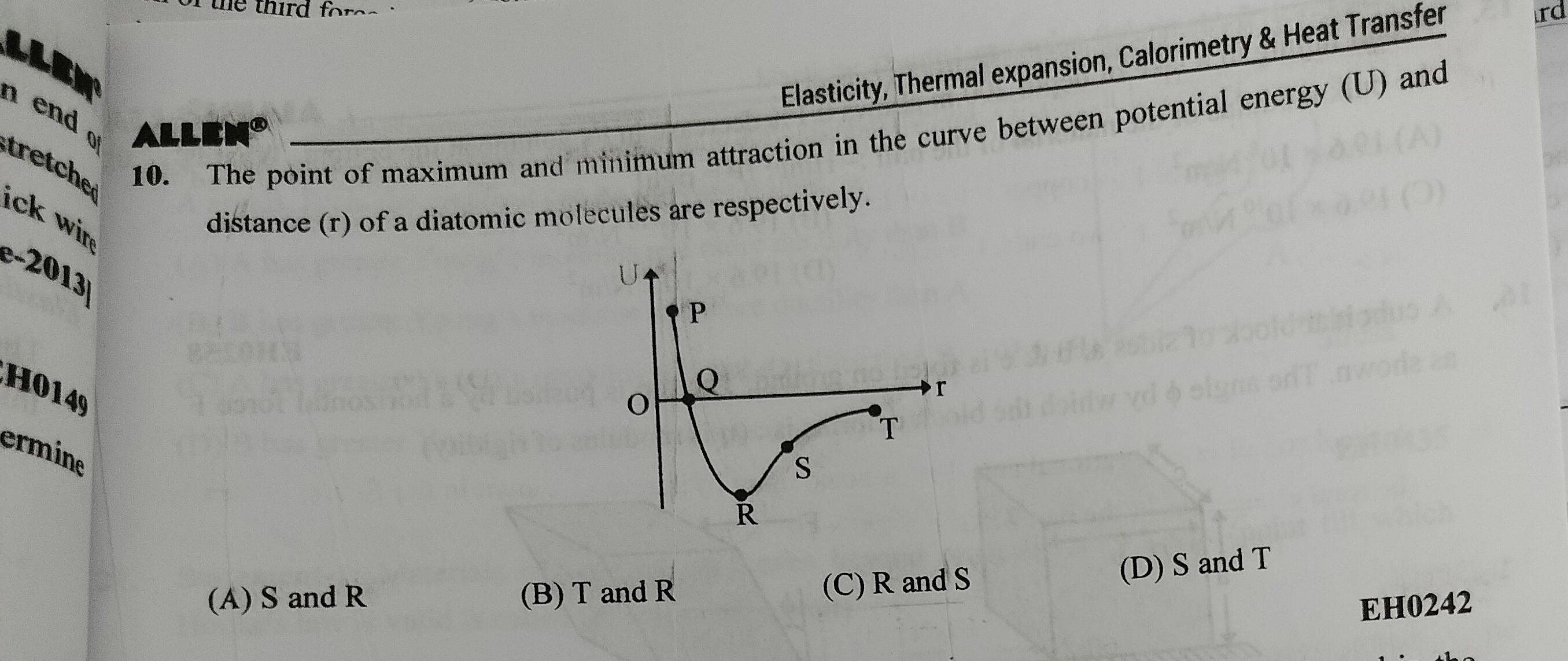
S and R
T and R
R and S
S and T
R and S
Solution
The force between two molecules is given by F=−drdU. Attraction occurs when F<0, which implies drdU>0. Repulsion occurs when F>0, which implies drdU<0. Equilibrium occurs when F=0, which implies drdU=0.
Point R represents the minimum of the potential energy curve, where the slope drdU=0. This signifies a point of stable equilibrium with zero net force.
For distances r>rR, the potential energy U increases with r, meaning drdU>0. This indicates an attractive force (F=−drdU<0).
The magnitude of the attractive force is ∣F∣=drdU. We need to find the point of maximum and minimum attraction.
Maximum Attraction: This corresponds to the most negative force, meaning the largest positive slope (drdU) in the attractive region. Observing the curve, point T has a steeper slope than point S, indicating a stronger attractive force at T. If we consider the possibility that R is being referred to in a context related to the onset of attraction after repulsion, and if there were a point of maximum attraction, it would be where the slope is steepest. However, among the given options, R is presented as a possibility for "maximum attraction". This is unconventional as R is equilibrium.
Minimum Attraction: This corresponds to the least negative force (closest to zero) in the attractive region. The attractive force increases from zero at R. Among the points S and T, S has a smaller slope than T, meaning the attractive force at S is weaker than at T. Therefore, S represents a point of minimum attraction among the labeled points in the attractive region.
Considering the options provided, and interpreting R as a reference point for equilibrium (zero force, which could be considered a boundary for attraction) and S as the point with the weakest attractive force among the labeled points in the attractive region, option (C) "R and S" becomes the most plausible answer, assuming the question intends to contrast the equilibrium point with a point of minimal attraction. The order is "maximum and minimum attraction respectively." If R is considered as a point related to maximum attraction (perhaps in a broader sense of the potential well), and S as minimum attraction, then (C) fits. A more standard interpretation would suggest T for maximum attraction and S for minimum attraction, leading to "T and S", which is not a direct option in that order. Given the options, the interpretation that R is the point of stable equilibrium (zero force) and S is the point of minimum attraction in the attractive region is the most likely intended meaning for option (C).
