Question
Question: Eight charges having the values as shown in the figure are arranged symmetrically on a circle of rad...
Eight charges having the values as shown in the figure are arranged symmetrically on a circle of radius 0.1 m. Potential at centre O will be
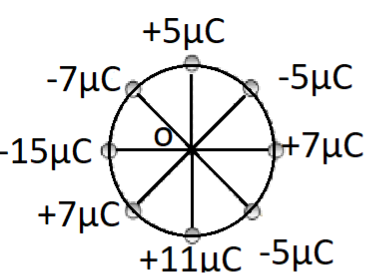
- 252×1010V
- 252×104V
- 252×106V
- Zero
Solution
In this question, all the charges are arranged symmetrically on the border of a circle of radius 0.1 m. So, we can apply the formula for the electric potential energy directly. Also, the net charge will be the direct sum of all the charges (with signs) due the symmetry.
Complete step by step answer:
By the formula for the electric potential energy at a pint
We have
Total potential at the centre O of the circle.
V=krq
Where, K is the Coulomb’s Constant, it is named after the scientist and founder of the electric potential, Charles-Augustin de Coulomb, a French military engineer and physicist
q is the net charge of the system
And, r is the distance
Here, q will be the sum of all the charges give to us
So,
V=4π∈01rqnet
Using the given charge values,
We have
⇒V=4π∈010.1(5−5+7−5+11+7+15−7)
⇒V=4π∈010.128
⇒V=9×1090.128
⇒V=252×1010
But,
The charges are given on micro scale
So,
⇒V=252×1010×10−6
⇒V=252×104V
So, the correct answer is “Option 2”.
Note: In this question, we have the charges that are given to us in the micro scale, but the options that are given to us are not in the micro scale. This can lead to the common misunderstanding or mistake that a student may make. Always pay attention to the units and make the correct conversion to get the correct answer. For example, for this case
1μC=10−6C
