Question

Effective resistance between A and B in the given circuit is

A. 6r
B. r
C. 2r
D. $\dfrac{r}{2}$

Answer 1

You could redraw the given circuit to find a Wheatstone bridge among the combination. Hence, one of the arms behaves as an open circuit and so the given circuit can again be simplified to get simple parallel and series combinations. Recall the expression for effective resistance for parallel and series combinations and hence solve the problem.

Formula used:
Expression for effective resistance:
In parallel, $\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$
In series, ${{R}_{eq}}={{R}_{1}}+{{R}_{2}}$

Complete step-by-step answer:
In the question we are given a little complex combination of resistors connected both in series and in parallel and we are asked to find the effective resistance across points A and B.
Before going directly into the question let us discuss finding the effective resistance at a basic level.
So, we have two basic combinations for resistors, namely, series and parallel. Two resistors are said to be connected in series when only one of their end points are joined to each other while they are said to be connected in parallel when both their ends are connected to each other.
Series:

The potential difference for a series connection is the sum of the potential difference across each resistor but the current remains constant throughout the combination. Also, by ohm’s law potential difference is given by the product of current and resistance.
$V={{V}_{1}}+{{V}_{2}}$
But, by ohm’s law,
$V=IR$
$\Rightarrow V=I\left( {{R}_{1}}+{{R}_{2}} \right)$
Comparing this with ohm’s law, we get the equivalent resistance for series combination as,
${{R}_{eq}}={{R}_{1}}+{{R}_{2}}$ …………………………. (1)
Parallel:

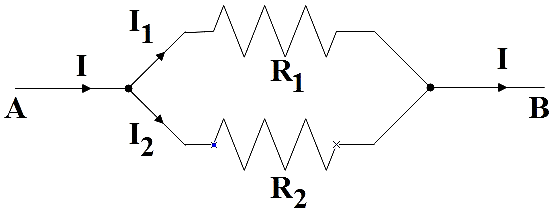
The potential difference across parallel connections is constant but current is different. So,
$I={{I}_{1}}+{{I}_{2}}$
$\dfrac{V}{{{R}_{eq}}}=\dfrac{V}{{{R}_{1}}}+\dfrac{V}{{{R}_{2}}}=V\left( \dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}} \right)$
Therefore, equivalent resistance for a parallel combination is,
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$ ……………………………… (2)
Now let us go to the given combination,

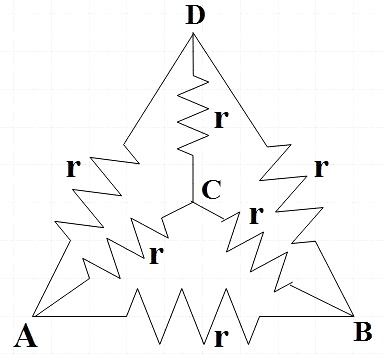
This can be redrawn as,

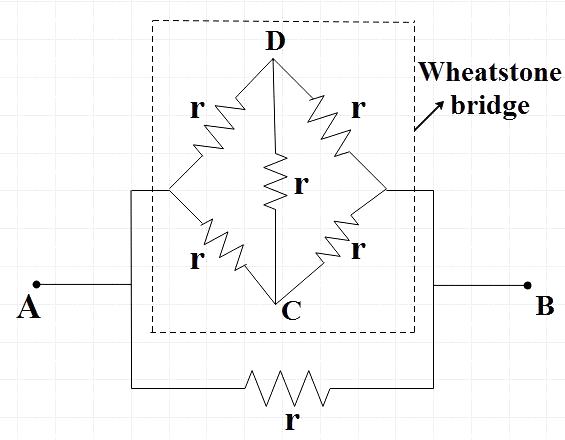
Now let us focus on the Wheatstone bridge part.

The Wheatstone bridge is an application of Kirchhoff’s law consisting of 4 resistors across one pair of diagonally opposite points which is further connected to a source. For the bridge to be in balanced condition,
$\dfrac{{{R}_{AD}}}{{{R}_{AC}}}=\dfrac{{{R}_{BD}}}{{{R}_{BC}}}$
$\Rightarrow \dfrac{r}{r}=\dfrac{r}{r}$
$\Rightarrow$ The given bridge is balanced.
A balanced Wheatstone bridge shows zero deflection in the galvanometer connected across CD which indicates that no current flows through ${{R}_{CD}}$ and it behaves as an open circuit across that arm.
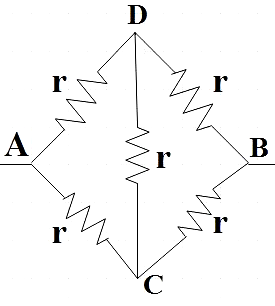
Now we can again redraw the circuit to get,

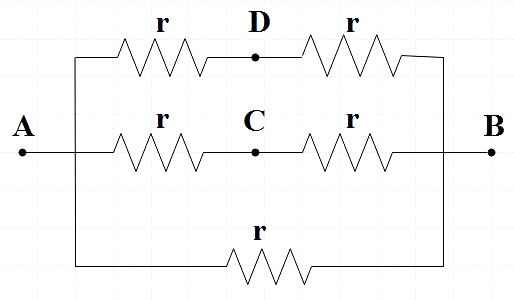
Effective resistance across arm ADB and ACB with two resistors of resistance r connected in series from (1),
${{R}_{ADB}}=r+r=2r$
${{R}_{ACB}}=r+r=2r$
Now we have three resistors connected parallel across A and B.

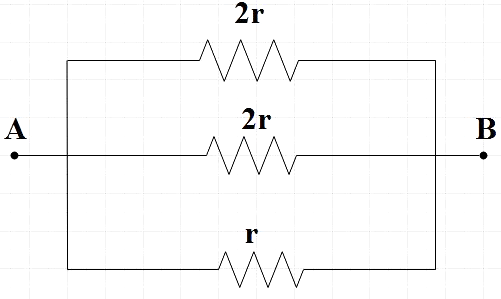
We could now find the effective resistance across A and B using (2).
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}$
$\Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{2r}+\dfrac{1}{2r}+\dfrac{1}{r}$
$\Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{1+1+2}{2r}$
$\Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{4}{2r}$
$\Rightarrow {{R}_{eq}}=\dfrac{1}{2}r$
Therefore, we get the effective resistance between A and B in the given circuit as,
${{R}_{eff}}=\dfrac{r}{2}$

So, the correct answer is “Option D”.

Note: The questions on finding effective resistance across two terminals may appear very complex at the first glance. But you could redraw the circuit in a more understandable manner and then approach each part step by step. The complex combinations may or may not contain a Wheatstone bridge, but if present makes it easy in finding the effective resistance.