Question

Calculate the velocity of the centre of mass of the system of particle shown in figure.

Answer 1

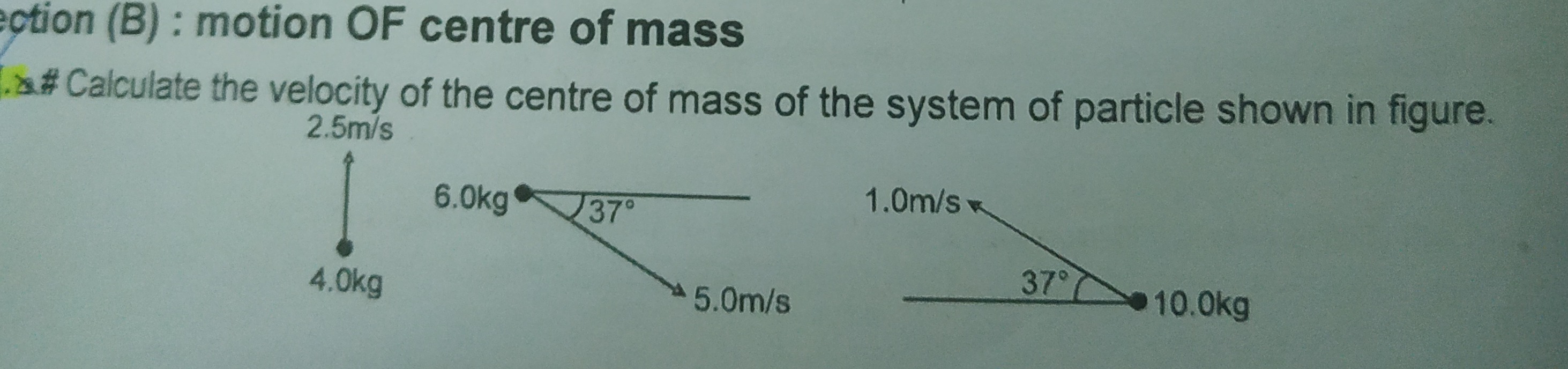
(0.8 \hat{i} - 0.1 \hat{j}) m/s

Answer 2

To calculate the velocity of the center of mass of the system, we use the formula:

$\vec{V}_{CM} = \frac{\sum m_i \vec{v}_i}{\sum m_i}$

First, let's identify the mass ($m_i$) and velocity vector ($\vec{v}_i$) for each particle. We'll set up a coordinate system where the positive x-axis is to the right and the positive y-axis is upwards. We'll use the standard approximations: $\sin 37^\circ \approx 0.6$ and $\cos 37^\circ \approx 0.8$.

Particle 1:

• Mass $m_1 = 4.0 \, \text{kg}$
• Velocity $v_1 = 2.5 \, \text{m/s}$ vertically upwards.
• $\vec{v}_1 = (0 \, \hat{i} + 2.5 \, \hat{j}) \, \text{m/s}$
• $m_1 \vec{v}_1 = 4.0 \, \text{kg} \times (0 \, \hat{i} + 2.5 \, \hat{j}) \, \text{m/s} = (0 \, \hat{i} + 10.0 \, \hat{j}) \, \text{kg} \cdot \text{m/s}$

Particle 2:

• Mass $m_2 = 6.0 \, \text{kg}$
• Velocity $v_2 = 5.0 \, \text{m/s}$ at an angle of $37^\circ$ below the horizontal, moving to the right.
• The x-component of velocity: $v_{2x} = v_2 \cos 37^\circ = 5.0 \times 0.8 = 4.0 \, \text{m/s}$
• The y-component of velocity: $v_{2y} = -v_2 \sin 37^\circ = -5.0 \times 0.6 = -3.0 \, \text{m/s}$ (negative because it's downwards)
• $\vec{v}_2 = (4.0 \, \hat{i} - 3.0 \, \hat{j}) \, \text{m/s}$
• $m_2 \vec{v}_2 = 6.0 \, \text{kg} \times (4.0 \, \hat{i} - 3.0 \, \hat{j}) \, \text{m/s} = (24.0 \, \hat{i} - 18.0 \, \hat{j}) \, \text{kg} \cdot \text{m/s}$

Particle 3:

• Mass $m_3 = 10.0 \, \text{kg}$
• Velocity $v_3 = 1.0 \, \text{m/s}$ at an angle of $37^\circ$ above the horizontal, moving to the left.
• The x-component of velocity: $v_{3x} = -v_3 \cos 37^\circ = -1.0 \times 0.8 = -0.8 \, \text{m/s}$ (negative because it's to the left)
• The y-component of velocity: $v_{3y} = v_3 \sin 37^\circ = 1.0 \times 0.6 = 0.6 \, \text{m/s}$
• $\vec{v}_3 = (-0.8 \, \hat{i} + 0.6 \, \hat{j}) \, \text{m/s}$
• $m_3 \vec{v}_3 = 10.0 \, \text{kg} \times (-0.8 \, \hat{i} + 0.6 \, \hat{j}) \, \text{m/s} = (-8.0 \, \hat{i} + 6.0 \, \hat{j}) \, \text{kg} \cdot \text{m/s}$

Next, calculate the total mass of the system: $M = m_1 + m_2 + m_3 = 4.0 \, \text{kg} + 6.0 \, \text{kg} + 10.0 \, \text{kg} = 20.0 \, \text{kg}$

Now, sum the momentum vectors ($\sum m_i \vec{v}_i$): $\sum m_i \vec{v}_i = (0 \, \hat{i} + 10.0 \, \hat{j}) + (24.0 \, \hat{i} - 18.0 \, \hat{j}) + (-8.0 \, \hat{i} + 6.0 \, \hat{j})$ Summing the x-components: $0 + 24.0 - 8.0 = 16.0 \, \text{kg} \cdot \text{m/s}$ Summing the y-components: $10.0 - 18.0 + 6.0 = -2.0 \, \text{kg} \cdot \text{m/s}$ So, $\sum m_i \vec{v}_i = (16.0 \, \hat{i} - 2.0 \, \hat{j}) \, \text{kg} \cdot \text{m/s}$

Finally, calculate the velocity of the center of mass: $\vec{V}_{CM} = \frac{(16.0 \, \hat{i} - 2.0 \, \hat{j}) \, \text{kg} \cdot \text{m/s}}{20.0 \, \text{kg}}$ $\vec{V}_{CM} = \left(\frac{16.0}{20.0}\right) \, \hat{i} - \left(\frac{2.0}{20.0}\right) \, \hat{j}$ $\vec{V}_{CM} = (0.8 \, \hat{i} - 0.1 \, \hat{j}) \, \text{m/s}$

The velocity of the center of mass of the system is $\vec{V}_{CM} = (0.8 \, \hat{i} - 0.1 \, \hat{j}) \, \text{m/s}$.