Question

Each resistance of the circuit shown in figure is r. The equivalent resistance between A and B is:

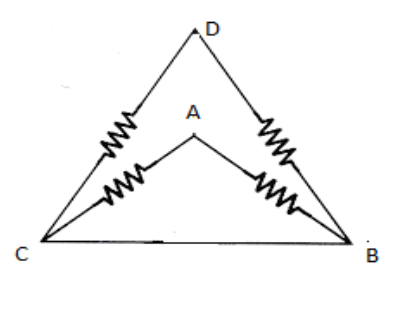
a) $r$
b) $\dfrac{r}{4}$
c) $\dfrac{r}{2}$
d) $\dfrac{5r}{8}$

Answer 1

Each resistance has the value r and then we will perform the summation using the rules of parallel and series combination.
Also for this problem we will use the concept that when a short circuit branch is connected in parallel with the other branches of the circuit then that branch will become ineffective to use.

Complete step by step answer:
In short circuit branch voltage becomes zero and when the two branches are connected in parallel it means both the branches have the same voltage. Therefore if one branch has zero voltage in it, then the other parallel connected branch too has zero voltage across it and hence we consider it as an ineffective branch.
Now, proceed for the calculation of the problem.
Branches AB and AC will become ineffective because both the branches are connected in parallel with the branch CB.
Then , we are left with branches DB and CD, which are now connected in parallel.
To sum up the parallel combination, we will take the reciprocal of both the resistors and then we will add the reciprocal of the resistors.
$\Rightarrow \dfrac{1}{r} + \frac{1}{r}$ (Reciprocal of the resistor values)
$\Rightarrow \dfrac{{r \times r}}{{r + r}}$ (We will take the LCM and then cancel the common terms)
$\Rightarrow \dfrac{r}{2}$

Hence, the correct answer is option (C).

Note: When the resistors are connected in series then their voltage magnitude will be different and the current through the circuit is the same. In order to find the equivalent resistance across the circuit the direct magnitude of the given resistors can be directly added.