Question
Question: Each of the segment of a prism frame is having resistance 2 $\Omega$, then net power generated in th...
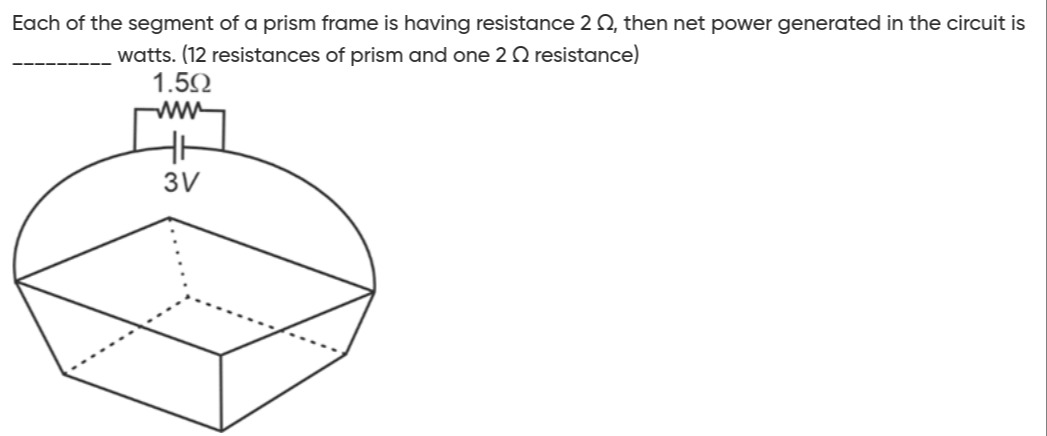
Each of the segment of a prism frame is having resistance 2 Ω, then net power generated in the circuit is ________ watts. (12 resistances of prism and one 2 Ω resistance)
Answer
2.84
Explanation
Solution
To solve this problem, we need to calculate the total equivalent resistance of the circuit and then use Ohm's law to find the total current, which will allow us to calculate the net power generated by the source.
1. Identify the components and their resistances:
- The circuit consists of a voltage source, an external resistance, and a prism frame made of resistive segments.
- The prism frame is a rectangular prism (cuboid). A cuboid has 12 edges.
- Each segment (edge) of the prism frame has a resistance of R0=2Ω.
- The voltage source is V=3V.
- There is an external resistance connected in series with the prism frame and the voltage source. The diagram shows this resistance as 1.5Ω. However, the text mentions "one 2 Ω resistance" in parentheses, which might refer to this external resistance. Given the ambiguity, we should prioritize the value explicitly shown in the diagram for the external resistance, which is 1.5Ω. If the intent was for it to be 2Ω, it should have been explicitly stated or drawn as such. We will proceed with Rext=1.5Ω.
2. Calculate the equivalent resistance of the prism frame (Rprism):
- The voltage source is connected across two opposite vertices of the prism frame, which means it's connected across a body diagonal.
- For a cube (or a rectangular prism with all edge resistances equal) where current enters at one vertex and leaves at the opposite vertex (body diagonal), the equivalent resistance is a standard result: Req=65R0 where R0 is the resistance of each edge.
- Given R0=2Ω: Rprism=65×2Ω=610Ω=35Ω.
3. Calculate the total equivalent resistance of the circuit (Rtotal):
- The prism frame (with its equivalent resistance Rprism) is connected in series with the external resistance Rext.
- Rtotal=Rprism+Rext
- Rext=1.5Ω=23Ω.
- Rtotal=35Ω+23Ω
- To add these fractions, find a common denominator, which is 6: Rtotal=3×25×2+2×33×3=610+69=619Ω.
4. Calculate the total current flowing in the circuit (I):
- Using Ohm's Law, I=RtotalV.
- I=619Ω3V=3×196A=1918A.
5. Calculate the net power generated in the circuit (P):
- The net power generated in the circuit is the power supplied by the voltage source.
- P=V×I
- P=3V×1918A=1954W.
6. Convert to decimal (if required):
- P=1954≈2.8421W.
- Rounding to two decimal places, P≈2.84W.
The final answer is 2.84
Explanation of the solution:
- Identify Resistances: Each of the 12 edges of the prism has a resistance of 2Ω. The external resistance is 1.5Ω.
- Equivalent Resistance of Prism: The source is connected across a body diagonal of the prism. The equivalent resistance of a cube (or prism with equal edge resistances) across a body diagonal is 65 times the resistance of a single edge. So, Rprism=65×2Ω=35Ω.
- Total Circuit Resistance: The prism's equivalent resistance is in series with the external resistance. Rtotal=Rprism+Rext=35Ω+1.5Ω=35+23=610+9=619Ω.
- Total Current: Using Ohm's Law, I=RtotalV=619Ω3V=1918A.
- Net Power Generated: Power generated by the source is P=V×I=3V×1918A=1954W≈2.84W.
