Question

Each month a store owner can spend at most 100,000 dollar on PC’s laptops. A PC cost the store owner 1000 dollar and a laptop cost him 1500 dollar. Each PC is sold for a profit of 400 dollar while a laptop is sold for a profit of 700 dollar. The store owner estimates that at least 15 PC’s but no more than 80 are sold each month. He also estimates that the number of laptops sold is at most half the PC’s. How many PC’s and how many laptops should be sold in order to maximize the profit?

Answer 1

Here we will use the concept of Linear Programming methods. We will assume the number of PC’s and the number of laptops to be some variable. First, we will find the equation of maximize profit and will form the constraints in which the value of assumed variable lies. Then we will form different inequalities by using the condition given to us. Finally, we will use all the conditions and constraints to find the desired answer.

Complete step by step solution:
Let $x$ and $y$ be the number of PC’s and laptops respectively. PC's are sold at a profit of $400$ and Laptops at profit of $700$. So our maximize Profit will be,
Profit $= 400x + 700y$
Next, it is given to us that number of PC’s should be at least 15 but not more than 80 and number of Laptops should be at most half of the PC’s so Constraints are,
$15 \le x \le 80$….$\left( 1 \right)$
$y \le \dfrac{1}{2}x$ ……$\left( 2 \right)$
This means $y \ge 0$ …..$\left( 3 \right)$
Then, it is given that store owner can spend total of 1,00,000 dollar on both PC’s and Laptops combined where Cost of one Pc’s is 1500 dollar and cost of one Laptop is 1500 so,
$1000x + 1500y \le 1,00,000$…..$\left( 4 \right)$
Now, we will plot all the above inequalities in a graph as below

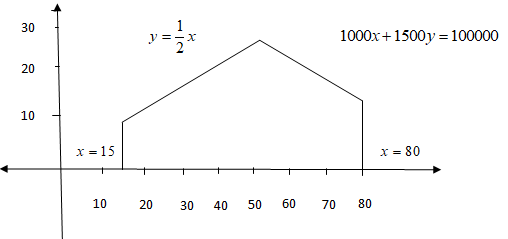
Now, let points at intersection of all the lines be named as,
At intersection of $x = 15$ and $y = 0$ ,$A:\left( {15,0} \right)$
At intersection of $x = 15$ and $y = \dfrac{1}{2}x$, $B:\left( {15,7.5} \right)$
At intersection of $y = \dfrac{1}{2}x$ and $1000x + 1500y = 100000$,$C:\left( {57.14,28.57} \right)$
At intersection of $1000x + 1500y = 100000$ and $x = 80$,$D:\left( {80,13.3} \right)$
So, we got our four points as: $A\left( {15,0} \right)$, $B\left( {15,7.5} \right)$,$C\left( {57.14,28.57} \right)$ and $D\left( {80,13.3} \right)$
Now we will calculate the profit at every point and check which of them is maximum.
The maximizing profit equation is Profit $= 400x + 700y$.
At Point $A\left( {15,0} \right)$, we get
Profit $= 400 \times 15 + 70 \times 0 = 6000$
At point $B\left( {15,7.5} \right)$, we get,
Profit $= 400 \times 15 + 700 \times 7.5 = 11250$
At point $C\left( {57.14,28.57} \right)$, we get,
Profit $= 400 \times 57.14 + 700 \times 7.5 = 42855$
At point $D\left( {80,13.3} \right)$ we get,
Profit $= 400 \times 80 + 700 \times 13.3 = 41310$
So, we get maximum profit at point $C$ and this point value of $x$ and $y$ is:
$x = 57.14,y = 28.57$
But as the number of PC’s and Laptops can’t be a decimal number, we will take the nearest value of $x$ and $y$ which satisfy all constraints.
So $x = 57$ and $y = 28$ satisfy all the constraints. Now,
Maximum Profit $= 500 \times 57 + 700 \times 28 = 42400$

So, the store owner should sell 57 PC’s and 28 Laptops for maximum profit.

Note:
Linear Programming method (LPP) is used to find the optimal value i.e. Maximum and Minimum value of linear Functions. The variable should be non-negative and should satisfy a set of linear inequalities so a graph or a relation between the inequalities can be formed to solve the problems. An LPP has many parts such as the objective function, Constraints, and Optimization Problems.