Question
Question: Each capacitor shown in figure has a capacitance of \[5.0\mu F\] . The emf of the battery is \[50V\]...
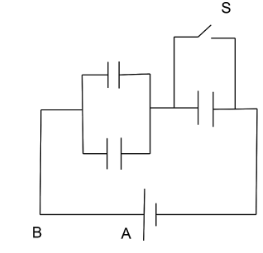
Each capacitor shown in figure has a capacitance of 5.0μF . The emf of the battery is 50V. How much charge will flow through AB if the switch S is closed?
Solution
the value of the capacitor connected to a switch will differ in the switched on and off conditions. When the switch is in the on state, the capacitor is assumed to be short but the charge is stored in it and doesn’t flow because it is considered short.
Formulas used:
Cparallel=C1+C2
⇒Cseries=C1+C2C1×C2
⇒Q=CV
Total charge= total charge when switch closed – total charge when switch open
Complete step by step answer:
The following data is given in the question: voltage, V=50V.
Capacitance of each capacitor is C=5.0μF
When S is open the capacitors in parallel produce a value of 10μF.
The 10μF capacitor is in series with the next 5μF capacitor.
The total value of capacitance is 10+510×5=1550=310μF.
The total charge can be found using the formula:
