Question

Each capacitor in the circuit shown is a $1F$ capacitor. What would be the equivalent capacitance between A and B

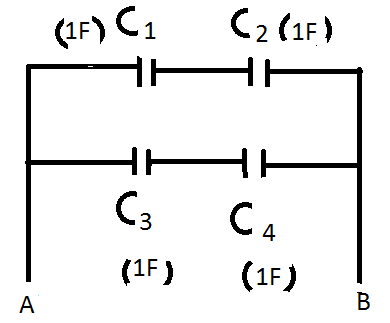
$(A)0.5F$
$(B)1F$
$(C)2F$
$(D)4F$

Answer 1

It can be solved by identifying which capacitors are in series and which sets are in parallel by using a formula for the equivalent capacitance for series and parallel combinations, we can get the equivalent capacitance between the required points.
Formula used:
Each capacitance of each pair of capacitance in series = $\dfrac{{{C_1} \times {C_2}}}{{{C_1} + {C_2}}}F$

Complete step by step answer:
A capacitor is a device that stores electrical energy in an electric field. It is a passive electronic component with two terminals.
The effect of a capacitor is known as capacitance. While some capacitance exists between any two electrical conductors in proximity in a circuit, a capacitor is a component designed to add capacitance to a circuit.
A $1$-farad capacitor can store one coulomb (coo-lamb) of charge at $1$ volt. One amp represents a rate of electron flow of $1$ coulomb of electrons per second, so a $1$-farad capacitor can hold $1$ amp-second of electrons at $1$ volt. A $1$-farad capacitor would typically be pretty big.
A one-farad modern super-capacitor. The farad (symbol: F) is the SI-derived unit of electrical capacitance, the ability of a body to store an electrical charge. It is named after the English physicist Michael Faraday. In SI base units $1F$ = $1{s^4} \cdot {A^2} \cdot {m^{ - 2}} \cdot k{g^{ - 1}}.$

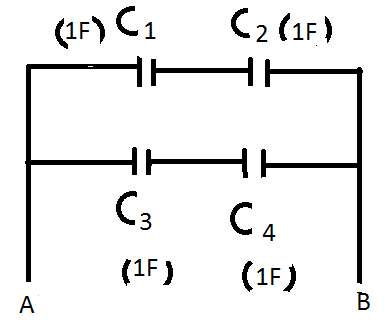
Where,
${C_1} = 1F$
${C_2} = 1F$
${C_3} = 1F$
${C_4} = 1F$
Each capacitance of each pair of capacitance in series = $\dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}}F$
Each capacitance of each pair of capacitance in series = $\dfrac{{1 \times 1}}{{1 + 1}}F = 0.5F$
The two series combination is connected in parallel. Hence the net capacitance becomes $0.5F + 0.5F = 1F$.

So, the correct answer is “Option C”.

Note: The equivalent capacitance is the net total capacitance of the capacitor connected in a circuit.
The equivalent has a large plate area and can therefore hold more charge than the individual capacitor.