Question
Question: $E_{Pb/Pb^{+2}}^{0} = -2\ V$ $E_{Pb^{+4}/Pb^{+2}}^{0} = -4\ V$ $E_{Pb/Pb^{+4}}^{0} = ?$...
EPb/Pb+20=−2 V
EPb+4/Pb+20=−4 V
EPb/Pb+40=?
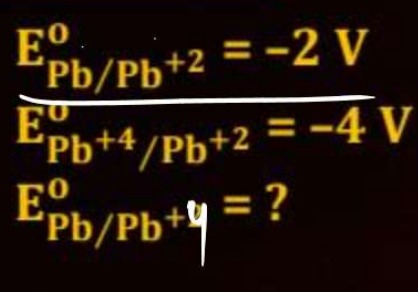
3 V
Solution
To solve this problem, we need to use the relationship between standard electrode potential (E0) and Gibbs free energy (ΔG0), which is given by the formula:
ΔG0=−nFE0
where n is the number of electrons transferred in the reaction and F is Faraday's constant. Since F is a constant, we can essentially work with nE0 values.
Standard electrode potentials are conventionally given as standard reduction potentials. Let's interpret the given potentials accordingly:
-
EPb/Pb+20=−2 V: This notation refers to the reduction potential for the half-reaction Pb+2+2e−→Pb.
Reaction (1): Pb+2+2e−→Pb
E10=−2 V
n1=2
ΔG10=−n1FE10=−(2)F(−2)=4F
-
EPb+4/Pb+20=−4 V: This notation refers to the reduction potential for the half-reaction Pb+4+2e−→Pb+2.
Reaction (2): Pb+4+2e−→Pb+2
E20=−4 V
n2=2
ΔG20=−n2FE20=−(2)F(−4)=8F
We need to find EPb/Pb+40. This refers to the standard oxidation potential for the reaction Pb→Pb+4+4e−. To find this, first, let's find the standard reduction potential for the corresponding reduction reaction: Pb+4+4e−→Pb. Let's call this Reaction (3).
Reaction (3): Pb+4+4e−→Pb
n3=4
ΔG30=−n3FE30=−(4)FE30
We can obtain Reaction (3) by adding Reaction (1) and Reaction (2):
(Pb+2+2e−→Pb)+(Pb+4+2e−→Pb+2)
Summing these gives: Pb+4+4e−→Pb
Since Gibbs free energy is an extensive property, the ΔG0 for the combined reaction is the sum of the ΔG0 values of the individual reactions:
ΔG30=ΔG10+ΔG20
ΔG30=4F+8F=12F
Now, substitute this value into the equation for ΔG30:
12F=−(4)FE30
Divide both sides by F:
12=−4E30
E30=−412=−3 V
This value, E30=−3 V, is the standard reduction potential for Pb+4/Pb, i.e., EPb+4/Pb0=−3 V.
The question asks for EPb/Pb+40, which is the standard oxidation potential for Pb→Pb+4+4e−. The standard oxidation potential is the negative of the standard reduction potential:
EPb/Pb+40=−EPb+4/Pb0
EPb/Pb+40=−(−3 V)=3 V
