Question

A 4 kg particle moves along the X-axis. It's position x varies with time according to

$x(t) = 2[1+36t+12t^2]$ where x is in m and t is in seconds. Compute:

(i) The kinetic energy at time t. $4t^6$ (ii) The force acting on the particle at time t. $48$ (iii) The power delivered to the particle at time t. $48t+288t^3$ (iv) The work done on the particle from t=0 to t=2 seconds. $1728$

Answer 1

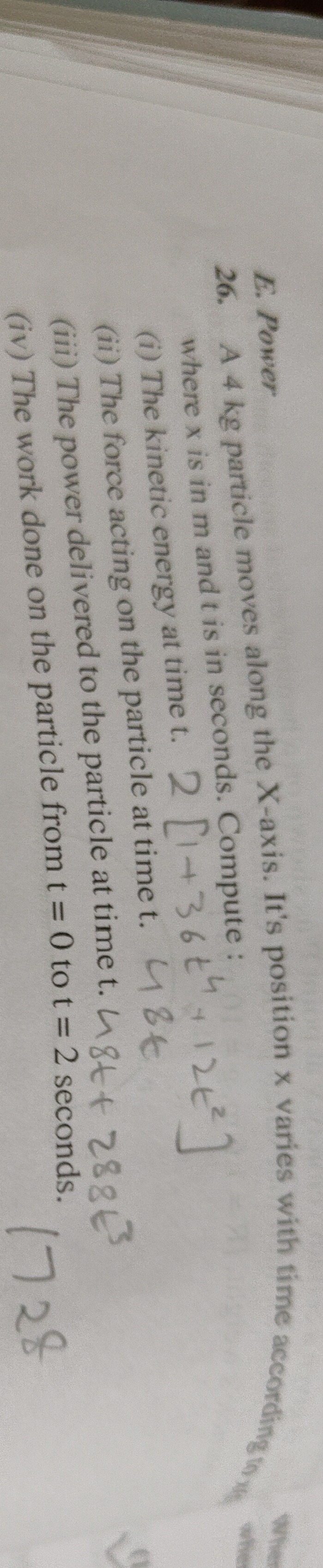
(i) The kinetic energy at time t: $1152 (3 + 2t)^2 \text{ J}$

(ii) The force acting on the particle at time t: $192 \text{ N}$

(iii) The power delivered to the particle at time t: $(13824 + 9216t) \text{ W}$

(iv) The work done on the particle from t=0 to t=2 seconds: $46080 \text{ J}$

Answer 2

The problem involves analyzing the motion of a particle along the X-axis given its position as a function of time. We will use calculus (differentiation and integration) and fundamental physics principles to compute kinetic energy, force, power, and work done.

1. Given Information:

• Mass of the particle, $m = 4 \text{ kg}$
• Position of the particle, $x(t) = 2[1+36t+12t^2] \text{ m}$ This can be expanded as $x(t) = 2 + 72t + 24t^2 \text{ m}$.

2. Calculate Velocity $v(t)$: Velocity is the first derivative of position with respect to time: $v(t) = \frac{dx}{dt} = \frac{d}{dt}(2 + 72t + 24t^2)$ $v(t) = 0 + 72 + 24(2t)$ $v(t) = (72 + 48t) \text{ m/s}$

3. Calculate Acceleration $a(t)$: Acceleration is the first derivative of velocity with respect to time: $a(t) = \frac{dv}{dt} = \frac{d}{dt}(72 + 48t)$ $a(t) = 0 + 48$ $a(t) = 48 \text{ m/s}^2$ The acceleration is constant.

---

Computations:

(i) The kinetic energy at time t: Kinetic energy (KE) is given by the formula $KE = \frac{1}{2}mv^2$. $KE(t) = \frac{1}{2} (4 \text{ kg}) (72 + 48t)^2$ $KE(t) = 2 (72 + 48t)^2$ We can factor out 24 from $(72 + 48t)$: $72 + 48t = 24(3 + 2t)$. $KE(t) = 2 [24(3 + 2t)]^2$ $KE(t) = 2 \times 24^2 (3 + 2t)^2$ $KE(t) = 2 \times 576 (3 + 2t)^2$ $KE(t) = 1152 (3 + 2t)^2 \text{ J}$

(ii) The force acting on the particle at time t: According to Newton's second law, force $F = ma$. $F(t) = (4 \text{ kg}) (48 \text{ m/s}^2)$ $F(t) = 192 \text{ N}$ The force acting on the particle is constant.

(iii) The power delivered to the particle at time t: Power $P$ is the dot product of force and velocity, $P = \vec{F} \cdot \vec{v}$. Since the motion is along the X-axis, the force and velocity are collinear, so $P = Fv$. $P(t) = F(t) \times v(t)$ $P(t) = (192 \text{ N}) (72 + 48t \text{ m/s})$ $P(t) = 192 \times 72 + 192 \times 48t$ $P(t) = 13824 + 9216t \text{ W}$

(iv) The work done on the particle from t=0 to t=2 seconds: Work done can be calculated using the Work-Energy Theorem ($W = \Delta KE$) or by integrating power over time ($W = \int P(t) dt$). We will use the latter method. $W = \int_{t_1}^{t_2} P(t) dt$ $W = \int_{0}^{2} (13824 + 9216t) dt$ $W = \left[13824t + \frac{9216t^2}{2}\right]_{0}^{2}$ $W = \left[13824t + 4608t^2\right]_{0}^{2}$ Now, substitute the limits: $W = (13824 \times 2 + 4608 \times 2^2) - (13824 \times 0 + 4608 \times 0^2)$ $W = (27648 + 4608 \times 4) - 0$ $W = 27648 + 18432$ $W = 46080 \text{ J}$