Question

E.M.F and the internal resistance of a cell are 1.1V and $0.5\Omega$ respectively. The cell e.m.f balances against 220cm of a potentiometer wire. On drawing a current ‘x’ from the cell, the balancing length reduces to 200cm, then:
A. x=1A
B. x=0.1A
C. x=0.5A
D. x=0.2A

Answer 1

Using the expression for potential difference between two points at distance l, express the given potential differences in terms of their respective balancing length. We can now express the potential difference when the current is drawn in terms of EMF of the cell and its internal resistance. Now by rearranging this relation and then substituting the given values, we get the value of the drawn current.

Formula used:
Expression for potential difference,
$V=\varepsilon -iR$
Between two points at distance l,
$\varepsilon \left( l \right)=\phi l$

Complete step by step answer:
We are given the E.M.F and the internal resistance of a cell. Now we are balancing the E.M.F against 220cm of a potentiometer wire. Now a current x is drawn from the cell, by using a potentiometer again we find that the balancing length is reduced to 200cm. We are asked to find the current x drawn from the cell.

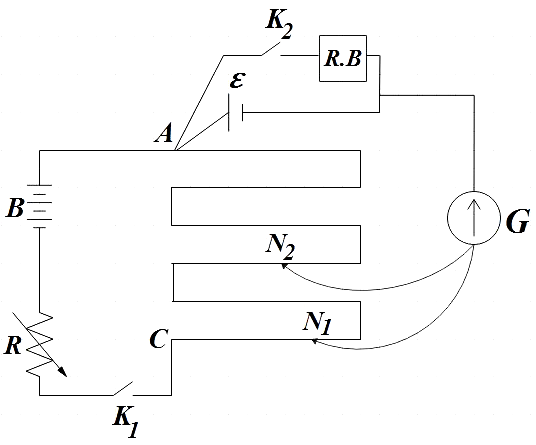
A current ‘$i$’ flows through the wire that is varied by using a rheostat (R) in the circuit. Assuming that the wire is uniform, the potential difference between A and any point at a distance l from A is,
$\varepsilon \left( l \right)=\phi l$ …………………………… (1)
Where, ‘$\phi$’ is the potential drop per unit length.
When cell of internal resistance $r=0.5\Omega$ is connected across a resistance box through key${{K}_{2}}$
When the key ${{K}_{2}}$ is open, the balance length is found to be the distance from A to${{N}_{1}}$, that is, ${{l}_{1}}$
So from (1),
$\varepsilon =\phi {{l}_{1}}$ ………………….. (2)
When the key ${{K}_{2}}$ is closed, a current ‘$x$’ is drawn , so, if V is the potential difference of the cell then balance length is the distance between A to ${{N}_{2}}$, that is, ${{l}_{2}}$
$\Rightarrow V=\phi {{l}_{2}}$ ……………………… (3)
Dividing (2) by (3),
$\dfrac{\varepsilon }{V}=\dfrac{{{l}_{1}}}{{{l}_{2}}}$
But, $V=\varepsilon -xr$
$\dfrac{\varepsilon }{\varepsilon -xr}=\dfrac{{{l}_{1}}}{{{l}_{2}}}$
$\Rightarrow \dfrac{1.1}{1.1-0.5x}=\dfrac{220}{200}$
$\Rightarrow 1.1-0.5x=\dfrac{1.1\times 200}{220}$
$\Rightarrow 0.5x=1.1-1=0.1$
$\therefore x=0.2A$
Therefore, the current drawn from the cell such that the balancing length reduced to 200cm is 0.2A.
Hence, option D is the answer.

Note:
Potentiometer is known to be a versatile instrument. It basically consists of a long uniform wire across which we connect a standard cell. The wire may be sometimes cut in several pieces and then placed side by side after which a thick metal strip is used to connect their ends.