Question

f(x)=x^2-5x+6; x \geq 5/2

Answer 1

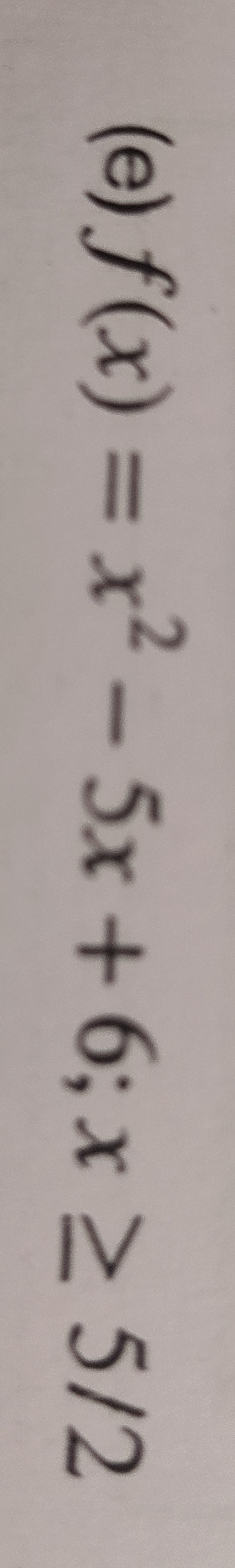
f^{-1}(x) = \frac{5 + \sqrt{1 + 4x}}{2}

Answer 2

The question provides a function $f(x) = x^2 - 5x + 6$ with a restricted domain $x \geq 5/2$. The specific task required for this function is not mentioned in the prompt. However, given the context of JEE/NEET exams, common questions involving such functions with restricted domains include finding the range, checking if the function is one-to-one, and finding the inverse function. We will perform these analyses.

1. Analysis of the function: The function is a quadratic $f(x) = x^2 - 5x + 6$. This is a parabola opening upwards. The vertex of the parabola is located at $x = -\frac{b}{2a} = -\frac{-5}{2(1)} = \frac{5}{2}$. The given domain is $x \geq 5/2$, which means we are considering the right half of the parabola starting from the vertex.

2. Monotonicity: Let's find the derivative of the function: $f'(x) = \frac{d}{dx}(x^2 - 5x + 6) = 2x - 5$. For the given domain $x \geq 5/2$, we have $2x \geq 5$, so $2x - 5 \geq 0$. $f'(x) = 0$ at $x = 5/2$, and $f'(x) > 0$ for $x > 5/2$. This indicates that the function is strictly increasing on the domain $[5/2, \infty)$.

3. Range: Since the function is strictly increasing on $[5/2, \infty)$, its minimum value occurs at the left endpoint of the domain, i.e., at the vertex $x = 5/2$. $f(5/2) = (5/2)^2 - 5(5/2) + 6 = \frac{25}{4} - \frac{25}{2} + 6 = \frac{25 - 50 + 24}{4} = -\frac{1}{4}$. As $x \to \infty$, $f(x) = x^2 - 5x + 6 \to \infty$. Therefore, the range of the function $f(x)$ for $x \geq 5/2$ is $[-1/4, \infty)$.

4. One-to-one property: A function is one-to-one (injective) if it is strictly monotonic on its domain. Since $f(x)$ is strictly increasing on $[5/2, \infty)$, it is one-to-one on this domain.

5. Inverse function: Since the function is one-to-one on the given domain, its inverse exists. Let $y = f(x)$. $y = x^2 - 5x + 6$. To find the inverse, we need to solve for $x$ in terms of $y$. We can complete the square or use the quadratic formula. Using the quadratic formula for $x^2 - 5x + (6 - y) = 0$: $x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4(1)(6 - y)}}{2(1)} = \frac{5 \pm \sqrt{25 - 24 + 4y}}{2} = \frac{5 \pm \sqrt{1 + 4y}}{2}$. The domain of $f$ is $x \geq 5/2$. We must choose the solution for $x$ that satisfies this condition. We have two potential expressions for $x$: $\frac{5 + \sqrt{1 + 4y}}{2}$ and $\frac{5 - \sqrt{1 + 4y}}{2}$. For $x \geq 5/2$, we need $\frac{5 \pm \sqrt{1 + 4y}}{2} \geq \frac{5}{2}$, which simplifies to $5 \pm \sqrt{1 + 4y} \geq 5$, or $\pm \sqrt{1 + 4y} \geq 0$. Since the square root $\sqrt{1 + 4y}$ is always non-negative (for $y$ in the range $[-1/4, \infty)$, $1+4y \geq 0$), the '+' sign must be chosen to satisfy $\pm \sqrt{1 + 4y} \geq 0$. Thus, $x = \frac{5 + \sqrt{1 + 4y}}{2}$. This expression gives the value of $x$ for a given value of $y$, which is the inverse function. Let $f^{-1}(y) = \frac{5 + \sqrt{1 + 4y}}{2}$. Replacing the variable $y$ with $x$ (standard notation for the independent variable of the inverse function): $f^{-1}(x) = \frac{5 + \sqrt{1 + 4x}}{2}$. The domain of the inverse function $f^{-1}(x)$ is the range of the original function $f(x)$, which is $[-1/4, \infty)$. The range of the inverse function $f^{-1}(x)$ is the domain of the original function $f(x)$, which is $[5/2, \infty)$.

In summary, for the function $f(x) = x^2 - 5x + 6$ with domain $x \geq 5/2$:

• It is a strictly increasing function.
• Its range is $[-1/4, \infty)$.
• It is one-to-one.
• Its inverse function is $f^{-1}(x) = \frac{5 + \sqrt{1 + 4x}}{2}$, with domain $[-1/4, \infty)$ and range $[5/2, \infty)$.

Since the question did not specify what needed to be solved, we have provided a comprehensive analysis of the function on the given domain, including finding its range, checking its injectivity, and determining its inverse. Assuming the question implicitly asked for the inverse function, this is the most likely intended solution.