Question

$\sin^{-1}\left(\sin\frac{2\pi}{3}\right) + \cos^{-1}\left(\cos\frac{7\pi}{6}\right) + \tan^{-1}\left(\tan\frac{3\pi}{4}\right)$ is equal to [2022]

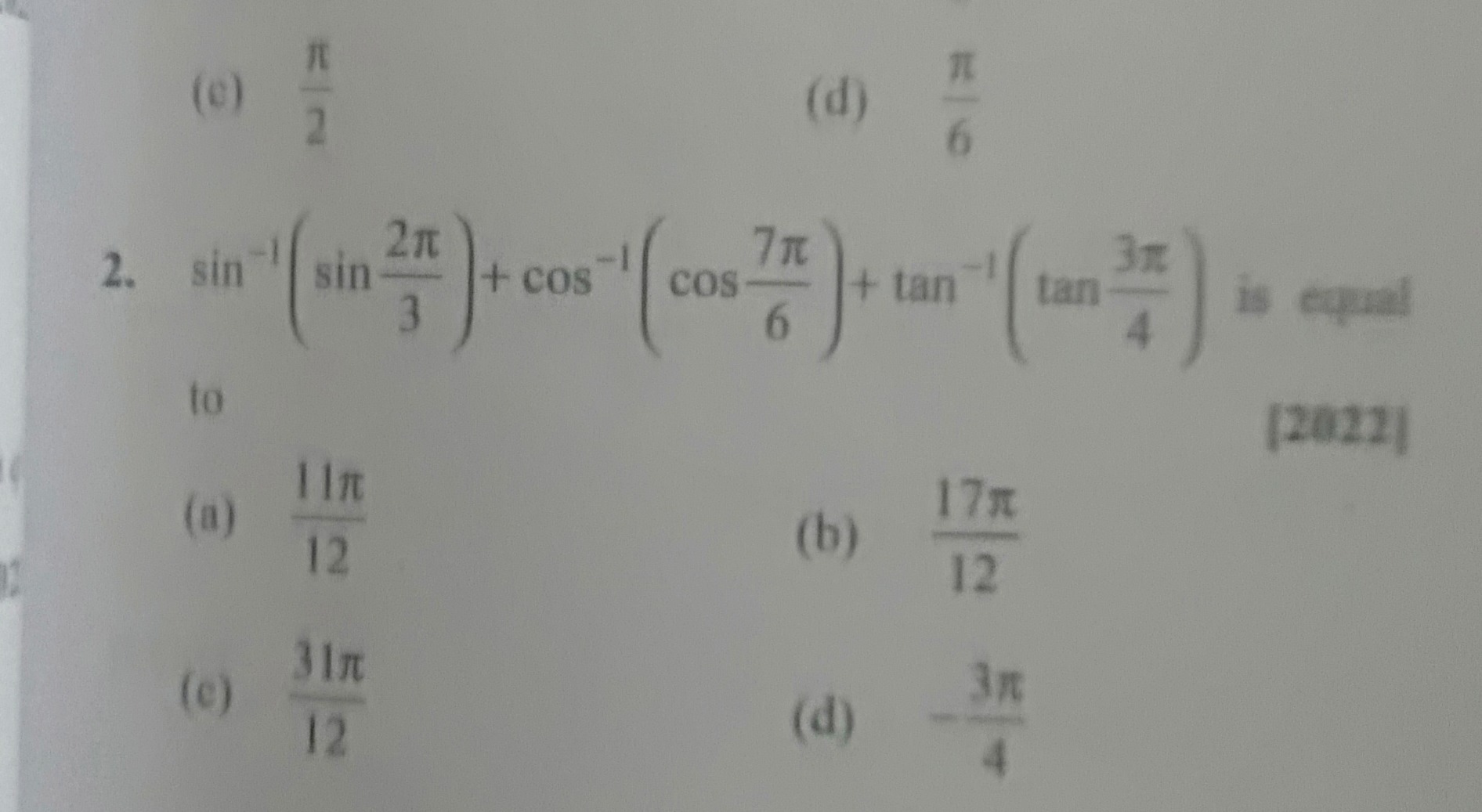
• A. $\frac{11\pi}{12}$
• B. $\frac{17\pi}{12}$
• C. $\frac{31\pi}{12}$
• D. $-\frac{3\pi}{4}$

Answer 1

Answer: (A)

$\frac{11\pi}{12}$

Answer 2

1. Evaluate each term:

   • $\sin^{-1}(\sin(2\pi/3))$:
     Since the range of $\sin^{-1}$ is $[-\pi/2, \pi/2]$ and $2\pi/3$ is outside this range, we use the identity:
     $\sin(2\pi/3) = \sin(\pi - 2\pi/3) = \sin(\pi/3)$.
     Hence, $\sin^{-1}(\sin(2\pi/3)) = \pi/3$.
2. • $\cos^{-1}(\cos(7\pi/6))$:
     The range of $\cos^{-1}$ is $[0,\pi]$.
     Since $\cos(7\pi/6) = \cos(π + π/6) = -\cos(π/6)$, the angle in $[0,\pi]$ with cosine $-\cos(π/6)$ is $5\pi/6$.
     Thus, $\cos^{-1}(\cos(7\pi/6)) = 5\pi/6$.
3. • $\tan^{-1}(\tan(3\pi/4))$:
     The range of $\tan^{-1}$ is $(-\pi/2,\pi/2)$.
     Note that $\tan(3\pi/4) = \tan(\pi - \pi/4) = -\tan(\pi/4) = -1$.
     So, $\tan^{-1}(\tan(3\pi/4)) = -\pi/4$.

4. Sum the results:

   $$\pi/3 + 5\pi/6 - \pi/4 = \frac{4\pi}{12} + \frac{10\pi}{12} - \frac{3\pi}{12} = \frac{11\pi}{12}.$$