Question
Question: E-4. (log₂10) . (log₂80) - (log₂5) . (log₂160) is equal to :...
E-4. (log₂10) . (log₂80) - (log₂5) . (log₂160) is equal to :
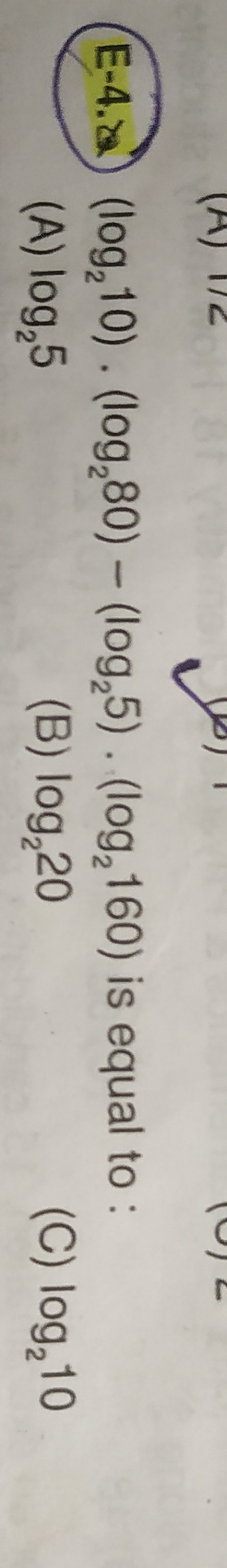
log₂5
log₂20
log₂10
The expression evaluates to 4, which is equivalent to log₂16. None of the provided options match this result.
Solution
Let the given expression be E. E=(log210)⋅(log280)−(log25)⋅(log2160)
We use the properties of logarithms: logb(xy)=logbx+logby and logbbn=n. Let's express the numbers inside the logarithms in terms of powers of 2 and 5. 10=2×5 80=16×5=24×5 160=32×5=25×5
Now, let's express each logarithmic term: log210=log2(2×5)=log22+log25=1+log25 log280=log2(24×5)=log224+log25=4log22+log25=4+log25 log25=log25 log2160=log2(25×5)=log225+log25=5log22+log25=5+log25
Let x=log25. Substitute these expressions into the given expression E: E=(1+x)(4+x)−(x)(5+x)
Now, expand and simplify the expression: E=(1×4+1×x+x×4+x×x)−(x×5+x×x) E=(4+x+4x+x2)−(5x+x2) E=(4+5x+x2)−(5x+x2) E=4+5x+x2−5x−x2 E=4
The value of the expression is 4. This is equivalent to log216.
