Question

If acceleration due to gravity on the surface of earth is 10 ms$^{-2}$ and acceleration due to gravitational acceleration at surface of another planet of our solar system be 5 ms$^{-2}$. An astronaut weighing 50 kg on earth goes to this planet in a spaceship with a constant velocity. The weight of the astronaut with time of flight is roughly given by

$KE = \frac{GMm}{2r}$

$PE = - \frac{GMm}{r}$

$TE = -\frac{GMm}{2r}$

(+ve) $\alpha \frac{1}{r}$

(-ve) $|PE| = 2|KE|$

(-ve) $TE = |RE|$

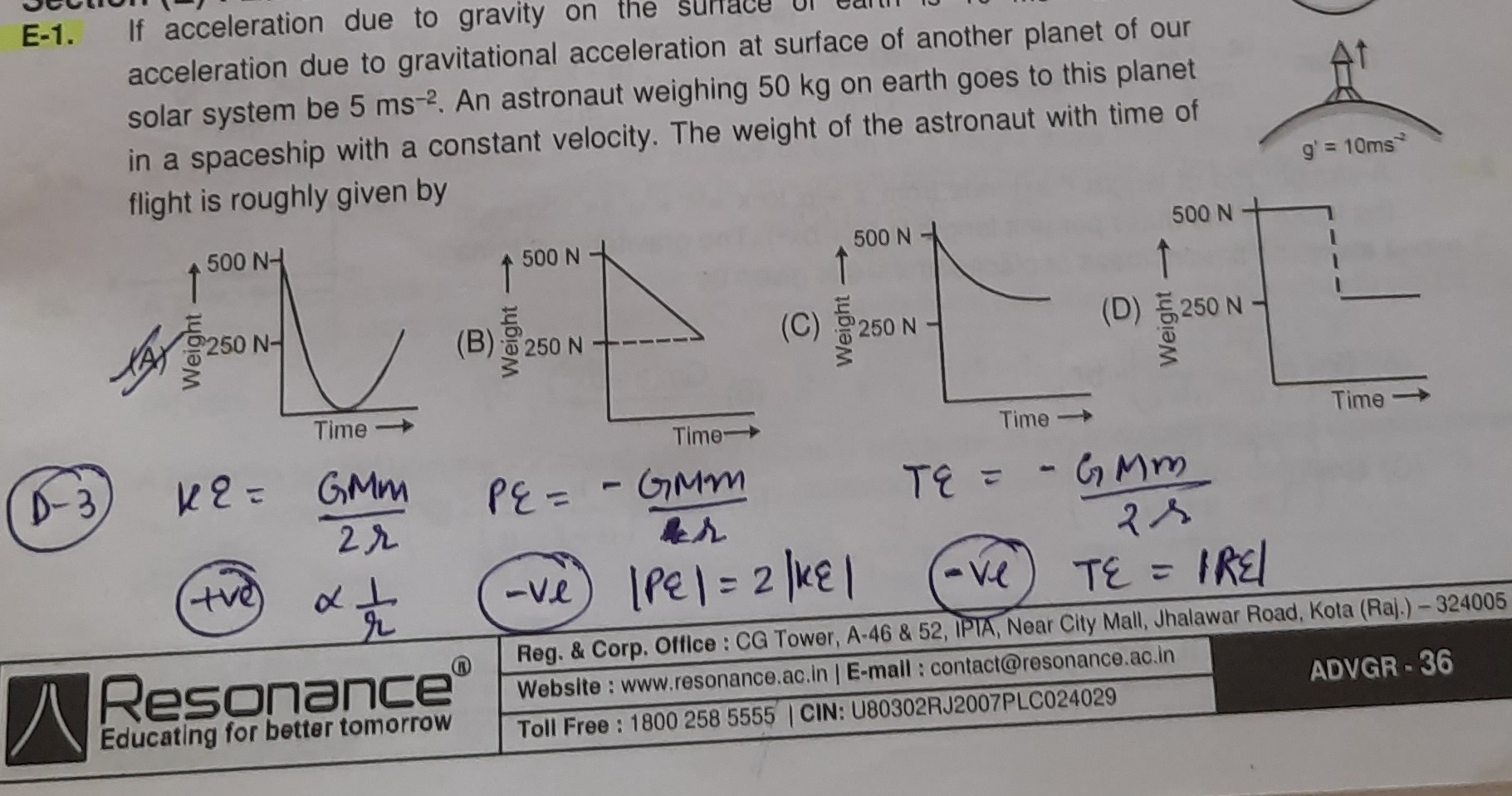
• A. Graph (A)
• B. Graph (B)
• C. Graph (C)
• D. Graph (D)

Answer 1

Answer: (A)

Graph (A)

Answer 2

The problem requires determining how the astronaut's weight changes during the journey from Earth to another planet.

1. Initial weight on Earth:

   • Mass of astronaut (m) = 50 kg
   • Acceleration due to gravity on Earth (g_e) = 10 ms⁻²
   • Weight on Earth (W_e) = m × g_e = 50 kg × 10 ms⁻² = 500 N

2. Final weight on the other planet:

   • Acceleration due to gravity on the other planet (g_p) = 5 ms⁻²
   • Weight on the other planet (W_p) = m × g_p = 50 kg × 5 ms⁻² = 250 N

3. Analyzing the journey: As the astronaut travels, they move away from Earth and towards the new planet. The gravitational force exerted by Earth decreases, while the gravitational force exerted by the other planet increases. At some point, the gravitational pull from Earth and the other planet will be equal, resulting in weightlessness. After passing this point, the gravitational pull of the new planet becomes dominant, and the astronaut's effective weight increases until they land on the planet's surface.

4. Evaluating the graphs:

   • Graph (A): Starts at 500 N, decreases to a minimum value (close to 0 N, representing weightlessness), and then increases to 250 N. This accurately depicts the change in weight during such a journey.
   • Graph (B): Shows a linear decrease from 500 N to 250 N. Gravitational force does not change linearly with distance, and this graph does not show a period of weightlessness.
   • Graph (C): Shows an asymptotic decrease from 500 N towards 250 N. This shape is incorrect for gravitational force variation between two bodies and does not show weightlessness.
   • Graph (D): Shows a sudden drop from 500 N to 250 N after some time. This represents an abrupt change, not the continuous variation of gravitational force during space travel. It also does not account for weightlessness.

Therefore, Graph (A) is the most appropriate representation of the astronaut's weight with time of flight. The phrase "constant velocity" implies that the spaceship's thrust is not actively accelerating or decelerating the ship, and the observed weight changes are due to the varying gravitational fields.