Question
Question: During SHM, a particle has displacement \( x \) from mean position. If acceleration, kinetic energy ...
During SHM, a particle has displacement x from mean position. If acceleration, kinetic energy and excess potential energy are represented by a , k and U respectively, then choose the appropriate graph
(A)
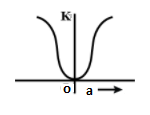
(B)
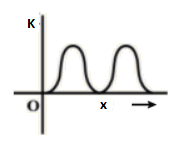
(C)
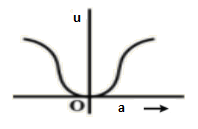
(D)
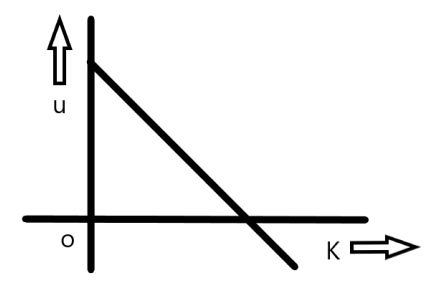
Solution
Hint
We write down the equations of kinetic energy and potential energy in a simple harmonic motion. Acceleration is then substituted into the formulas of kinetic and potential energy. These equations are compared to the graph to find which one of them is correct.
Formula used: kinetic energy k=21ω2(A2−x2)
Potential energy U=21mω2x2
Acceleration of particle a=ω2x
Here,Mass of particle is represented by m
Amplitude of particle is represented by A
Displacement is represented by x
Angular frequency is represented by ω
Kinetic energy is represented by k
Potential energy is represented by U .
Complete step by step answer
kinetic energy of a particle in a simple harmonic motion is given by
⇒k=21ω2(A2−x2)
⇒k=21(ω2A2−ax)
Potential energy is given by
⇒U=21mω2x2
⇒U=21m×a×x
Acceleration is given by a=ω2x
Taking graph (A) we can see that acceleration is zero at x equal to zero but from kinetic energy formula k=21(ω2A2−ax) . kinetic energy is not equal to zero at acceleration zero hence (A) is incorrect
The graph of kinetic energy vs displacement should be parabolic. which is not the case in option (B), so it is incorrect.
Potential energy is zero when acceleration is zero and maximum when acceleration is maximum which is satisfied by the equation of potential energy U=21m×a×x hence option (c) is correct.
The sum of kinetic and potential energy is always equal to
\begin{array}{*{20}{l}}
{\;U + K = \dfrac{1}{2}m{\omega ^2}{A^2}} \\\
{ \Rightarrow U = - K + \dfrac{1}{2}m{\omega ^2}{A^2}}
\end{array}
So it is a straight line with a negative slope and an intercept on the y-axis
Hence option (D) is correct.
Option (C) and (D) are correct.
Note
Simple harmonic motion is a special type of periodic motion where the restoring force on the moving object is directly proportional to the object's displacement magnitude and acts towards the object's equilibrium position.
